
 .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
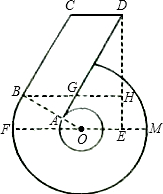 H∥FM,DH⊥BH于H,设∠FOB=α,OB=4,BC=6.
H∥FM,DH⊥BH于H,设∠FOB=α,OB=4,BC=6.查看答案和解析>>
科目:初中数学 来源: 题型:
(本小题满分8分)
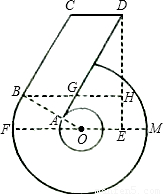
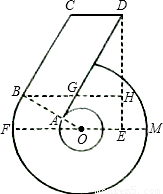
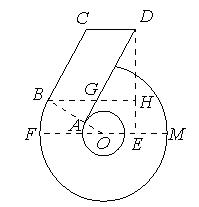
“6”字形图中,FM是大⊙O的直径,BC与大⊙O相切于B,
OB与小⊙O相交于点A,AD∥BC,CD∥BH∥FM,DH⊥BH于H,
设∠FOB=α,OB=4,BC=6.
(1)求证:AD为小⊙O的切线;
 (2)在图中找出一个可用α表示的角,并说明你这样表示的理由;(根据所写结果的正确性及所需推理过程的难易程度得分略有差异)
(2)在图中找出一个可用α表示的角,并说明你这样表示的理由;(根据所写结果的正确性及所需推理过程的难易程度得分略有差异)
(3)当α=30º时,求DH的长。(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
|
查看答案和解析>>
科目:初中数学 来源:2012年江西抚州市崇仁四中初三第二次月考数学试卷(带解析) 题型:解答题
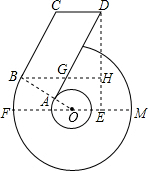
已知“6”字形图中,FM是大⊙O的直径, BC与大⊙O相切于B, OB与小⊙O相交于A, AD∥BC,CD∥BH∥FM, DH⊥BH于H,设∠FOB=30°,OB="4," BC=6.
﹙1﹚求证:AD为小⊙O的切线;
﹙2﹚求DH的长.﹙结果保留根号﹚
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com