
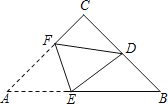
【题目】如图,在△ABC中,CA=CB,∠C=90°,点D是BC的中点,将△ABC沿着直线EF折叠,使点A与点D重合,折痕交AB于点E,交AC于点F,那么sin∠BED的值为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
先根据翻折变换的性质得到△DEF≌△AEF,再根据等腰三角形的性质及三角形外角的性质可得到∠BED=CDF,设CD=1,CF=x,则CA=CB=2,再根据勾股定理即可求解.
解:∵△DEF是△AEF翻折而成,
∴△DEF≌△AEF,∠A=∠EDF,
∵△ABC是等腰直角三角形,
∴∠EDF=45°,由三角形外角性质得∠CDF+45°=∠BED+45°,
∴∠BED=∠CDF,
设CD=1,CF=x,则CA=CB=2,
∴DF=FA=2-x,
∴在Rt△CDF中,由勾股定理得,CF2+CD2=DF2,即x2+1=(2-x)2,
解得x=![]() ,
,
∴sin∠BED=sin∠CDF=![]() =
=![]() ,
,


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
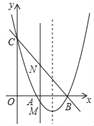
【题目】如图,抛物线y=x2+bx+c与x轴交于点A和B(3,0),与y轴交于点C(0,3).
(1)求抛物线的解析式;
(2)若点M是抛物线上在x轴下方的动点,过M作MN∥y轴交直线BC于点N,求线段MN的最大值;
(3)E是抛物线对称轴上一点,F是抛物线上一点,是否存在以A,B,E,F为顶点的四边形是平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
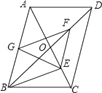
【题目】如图,平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②EG=EF;③△EFG≌△GBE;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的个数是( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
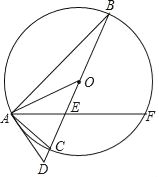
【题目】如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,延长BC到点D,连接OA,AD,使得∠FAC=∠AOD,∠D=∠BAF.
(1)求证:AD是⊙O的切线;
(2)若⊙O的半径为5,CE=2,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
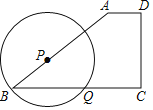
【题目】已知在梯形ABCD中,AD∥BC,AB=BC,DC⊥BC,且AD=1,DC=3,点P为边AB上一动点,以P为圆心,BP为半径的圆交边BC于点Q.
(1)求AB的长;
(2)当BQ的长为![]() 时,请通过计算说明圆P与直线DC的位置关系.
时,请通过计算说明圆P与直线DC的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某省计划5年内全部地级市通高铁.某高铁在泰州境内的建设即将展开,现有大量的沙石需要运输.某车队有载质量为8t、10t的卡车共12辆,全部车辆运输一次能运输100t沙石.
(1)求某车队载质量为8t、10t的卡车各有多少辆;
(2)随着工程的进展,某车队需要一次运输沙石165t以上,为了完成任务,准备新增购这两种卡车共7辆,车队有多少种购买方案?请你一一求出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 、
、![]() 、
、![]() 在直线
在直线![]() 上,点
上,点![]() 、
、![]() 、
、![]() 、
、![]() 在直线
在直线![]() 上,若
上,若![]() ,
,![]() 从如图所示的位置出发,沿直线
从如图所示的位置出发,沿直线![]() 向右匀速运动,直到
向右匀速运动,直到![]() 与
与![]() 重合.运动过程中
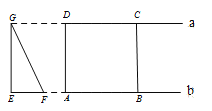
重合.运动过程中![]() 与矩形
与矩形![]() 重合部分的面积
重合部分的面积![]() 随时间
随时间![]() 变化的图象大致是( )
变化的图象大致是( )
A. 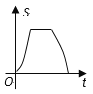 B.
B. 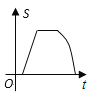 C.
C. 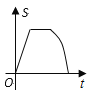 D.
D. 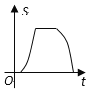
查看答案和解析>>
科目:初中数学 来源: 题型:
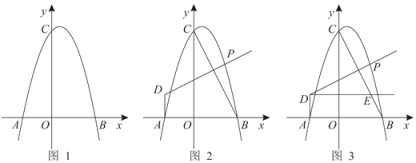
【题目】已知:如图,抛物线![]() 交x轴于A(-2,0),B(3,0)两点,交y轴于点C(0,6).
交x轴于A(-2,0),B(3,0)两点,交y轴于点C(0,6).
(1)写出a,b,c的值;
(2)连接BC,点P为第一象限抛物线上一点,过点A作AD⊥x轴,过点P作PD⊥BC于交直线AD于点D,设点P的横坐标为t,AD长为h.
①求h与t的函数关系式和h的最大值(请求出自变量t的取值范围);
②过第二象限点D作DE∥AB交BC于点E,若DP=CE,时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A:篮球 B:乒乓球C:羽毛球 D:足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:


(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com