
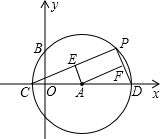
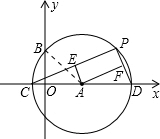
 如图,以(3,0)为圆心作⊙A,⊙A与y轴交于点B(2,0),与x轴交于C、D,P为⊙A上不同于C、D的任意一点,连接PC、PD,过A点分别作AE⊥PC于E,AF⊥PD于F.设点P的横坐标为x,AE2+AF2=y.当P点在⊙A上顺时针从点C运到点D的过程中,下列图象中能表示y与x的函数关系的图象是
如图,以(3,0)为圆心作⊙A,⊙A与y轴交于点B(2,0),与x轴交于C、D,P为⊙A上不同于C、D的任意一点,连接PC、PD,过A点分别作AE⊥PC于E,AF⊥PD于F.设点P的横坐标为x,AE2+AF2=y.当P点在⊙A上顺时针从点C运到点D的过程中,下列图象中能表示y与x的函数关系的图象是





 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
 A点运动,E为AB上一动点,点E以1cm/s的速度从A点出发向点B运动.
A点运动,E为AB上一动点,点E以1cm/s的速度从A点出发向点B运动.查看答案和解析>>
科目:初中数学 来源: 题型:
 |
| BF |
 |
| AB |
 |
| AF |
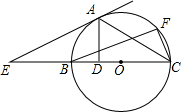 D,过A作AE∥BF交CB的延长线于E.
D,过A作AE∥BF交CB的延长线于E.| BD |
| CD |
| BE |
| EC |
| 1 |
| CD |
| 1 |
| EC |
| 2 |
| d |
查看答案和解析>>
科目:初中数学 来源: 题型:
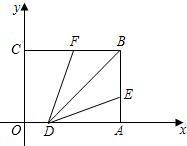
 (2012•张家港市模拟)如图,以矩形OABC的顶点O为坐标原点,OA所在的直线为x轴,OC所在的直线为y轴,建立直角坐标系.已知OA=3,OC=2,点E是AB的中点,点F在BC上,CF=1,点M、N分别是x轴、y轴上的动点,则四边形MEFN周长的最小值为
(2012•张家港市模拟)如图,以矩形OABC的顶点O为坐标原点,OA所在的直线为x轴,OC所在的直线为y轴,建立直角坐标系.已知OA=3,OC=2,点E是AB的中点,点F在BC上,CF=1,点M、N分别是x轴、y轴上的动点,则四边形MEFN周长的最小值为| 5 |
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com