
| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
分析 先将621分解因数,由于,$\frac{621xy}{x+y}$是整数,得出(x+y)只是621xy的约数,即可得出9个二元不定方程,针对于前8个,x+y是奇数,要使两个数的和是奇数,这两个加数中必有一个为偶数,而x,y是质数,偶数中只有2是质数,即,x,y中必有一个是2,求出另一个加数,再判断它是否是不同的质数,即可得出结论,针对于最后一个,用y表示出x,用x,y都是整数即可求出x,y的值,再判断是否是不同的质数,即可.
解答 解:621=3×207=9×69=23×27=1×621,
∵$\frac{621xy}{x+y}$是整数,且x,y是互不相同的质数,
∴(x+y)只是621xy的约数,
∴①x+y=3,当x=2时,y=3-x=1,而1不是质数,此种情况不符合题意,
同理:y=2时,也不符合题意,即:此种情况中不存在有序数对(x,y);
②x+y=207,当x=2时,y=207-x=205,而205不是质数,此种情况不符合题意,
同理:y=2时,也不符合题意,即:此种情况中不存在有序数对(x,y);
③x+y=9,∵当x=2时,y=9-x=7,而7是不等于2的质数,
∴有序数对为(2,7),
同理:当y=2时,有序数对为(7,2),共两种;
④x+y=69,∵当x=2时,y=69-x=67,而67是不等于2的质数,
∴有序数对为(2,67),
同理:当y=2时,有序数对为(67,2),共两种;
⑤x+y=23,当x=2时,y=23-x=21,而21不是质数,此种情况不符合题意,
同理:y=2时,也不符合题意,即:此种情况中不存在有序数对(x,y);
⑥x+y=27,当x=2时,y=27-x=5,而25不是质数,此种情况不符合题意,
同理:y=2时,也不符合题意,即:此种情况中不存在有序数对(x,y);
⑦x+y=1,∵x,y是互不相同的质数,此种情况不存在两个质数的和为1;
⑧x+y=621,∵当x=2时,y=621-x=619,而619是不等于2的质数,
∴有序数对为(2,619),
同理:当y=2时,有序数对为(619,2),共两种;
⑨x+y=xy,∴x=$\frac{y}{y-1}$,
∵x,y是整数数,
∴y-1=1,
∴y=2,
∴x=2,
∵x,y是互不相同的质数,所以舍去.
即:满足条件的有序数对(x,y)有(2,7),(7,2),(2,67),(67,2),(2,691),(619,2),共6种,
故选B.
点评 此题是质数与合数,主要考查了数的分解因数,一元一次方程的解法,确定出$\frac{621xy}{x+y}$是整数的x,y满足的条件是解本题的关键,而判断出两个质数的和是奇数时,必有一个加数是质数2,是解本题的难点,此题用到分类讨论的思想,是一道很好的竞赛题.


科目:初中数学 来源: 题型:解答题
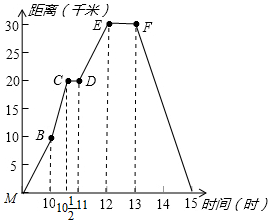 如图所示,折线表示小丽骑车离家的距离与时间的关系,小丽上午九时离开家,下午十五时到家,根据折线图所提供的信息,思考并回答下列问题:
如图所示,折线表示小丽骑车离家的距离与时间的关系,小丽上午九时离开家,下午十五时到家,根据折线图所提供的信息,思考并回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1,2,$\sqrt{3}$ | B. | 3,4,5 | C. | 1,1,$\sqrt{2}$ | D. | 6,12,13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
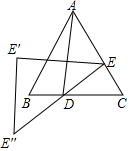 如图,在等边△ABC中,AB=4,D是BC边上任意一点(不与B,C重合),过点D作DE⊥AC,垂足为E,作点E关于直线AD对称的点E',作点E关于点D的对称点E″,作△EE'E″,当△EE'E″是轴对称图形时,S△EE'E″=48-24$\sqrt{3}$.
如图,在等边△ABC中,AB=4,D是BC边上任意一点(不与B,C重合),过点D作DE⊥AC,垂足为E,作点E关于直线AD对称的点E',作点E关于点D的对称点E″,作△EE'E″,当△EE'E″是轴对称图形时,S△EE'E″=48-24$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两个锐角对应相等 | B. | 一个锐角、一条直角边对应相等 | ||
| C. | 两条直角边对应相等 | D. | 一条斜边、一条直角边对应相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com