
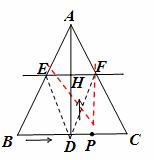
�� ͼ���ڡ�ABC�У�AB=AC��AD��AB��D��BC=10cm��AD=8cm����P�ӵ�B���������߶�BC����ÿ��3cm���ٶ����C�����˶������ͬʱ����ֱ��AD��ֱ��m�ӵױ�BC��������ÿ��2cm���ٶ���DA��������ƽ�ƣ��ֱ�AB��AC��AD��E��F��H������P�����Cʱ����P��ֱ��mͬʱֹͣ�˶������˶�ʱ��Ϊt�루t��0����
��1����t=2ʱ������DE��DF����֤���ı���AEDFΪ���Σ�
��2���������˶������У����γɵġ�PEF������������ֵ������PEF��������ʱ�����߶�BP�ij���
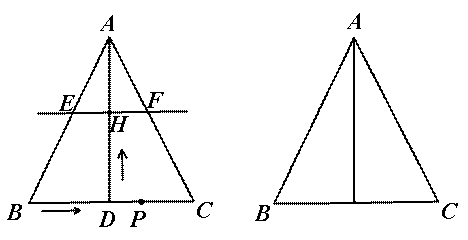 ��3���Ƿ����ijһʱ��t��ʹ��PEFΪֱ�������Σ������ڣ��������ʱ��t��ֵ���������ڣ���˵�����ɡ�
��3���Ƿ����ijһʱ��t��ʹ��PEFΪֱ�������Σ������ڣ��������ʱ��t��ֵ���������ڣ���˵�����ɡ�
��25-1ͼ ��25����ͼ
�⣺��1����t=2ʱ��DH=AH=4����AD��AB��AD��EF��֪EF��BC
�� 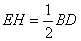 ��
��
�֡� AB=AC��AD��BC
�� BD=CD
�� EH=FH
�� EF��AD���ഹֱƽ��
�� �ı���AEDFΪ����
��2���������DH=2t��AH=8��2t��BC=10cm��AD=8cm����EF��BC֪��AEF�ס�ABC
�� 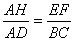 ��
��
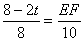 �����
�����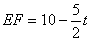
�� 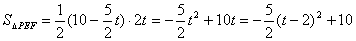
����PEF������������ֵ10cm2����ʱBP=3��2=6cm��
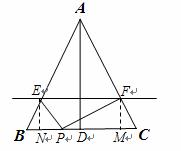
��3����E��F�ֱ���EN��BC��N��EM��BC��M����֪EF =MN=
=MN=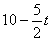
EN=FM����AB=AC��֪BN=CM=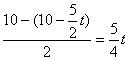
��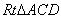 ��
��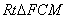 ����
����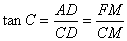 ��
��  ��
��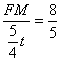 ��
��
���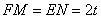 ������
������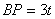 ֪
֪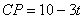 ��
��
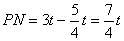 ��
��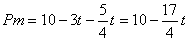
�� 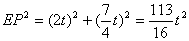 ��
�� 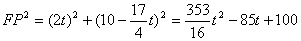
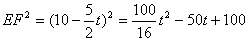
������������ۣ�
������EPF=90�㣬��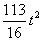
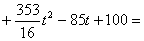
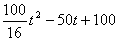 �����
�����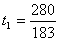 ��
��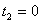 ����ȥ��
����ȥ��
������EFP=90�㣬��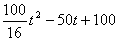
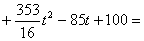
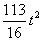 �����
�����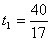 ��
��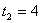 ����ȥ��
����ȥ��
������FEP=90�㣬��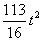

 �����
�����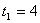 ��
��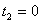 ������ȥ��
������ȥ��
������������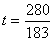
 ��
�� ʱ����PEFΪֱ�������Ρ�
ʱ����PEFΪֱ�������Ρ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
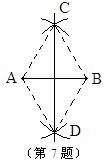
��ͼ��С�������߶�AB�Ĵ�ֱƽ����ʱ�������������ģ��ֱ��Ե�A��BΪԲ�ģ������߶�AB����һ��ij�Ϊ�뾶�������ཻ�ڵ�C��D����ֱ��CD��Ϊ��������AC��BC��AD��BD������������ͼ������֪���ı���ADBCһ����
A. ���� B. ����
C. ������ D. ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��k�ֱ�ȡ��1��1��2ʱ������y=��k��1��x2��4x+5��k�������ֵ����д������жϣ���˵�����ɣ����У���������ֵ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����20ͼ��ij��ѧ��ȤС�������һ����CD�ĸ߶ȣ��������ڵ�A���������C������Ϊ30�㣬Ȼ����AD����ǰ��10m������B�㣬��B���������C�����Ǹ߶�Ϊ60�㣨A��B��D������ͬһֱ���ϣ�������������Dz������ݼ��������CD�ĸ߶ȣ������ȷ��0.1m�������ο����ݣ�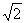 ��1.414��
��1.414��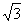 ��1.732��
��1.732��
 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ2����֪AC��BD����CAE=30�㣬��DBE=45 �����AEB����
�����AEB����
A��30�� B��45��C��60�� D��75��
 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com