如图所示，如果△APB绕点B按逆时针方向旋转30°后得到△A＇P＇B，且BP=2，那么点P与点P＇间的长度为___________． (不取近似值. 以下数据供解题使用：sin 15°=，cos 15°=)
科目：初中数学 来源： 题型：
根据图中所给的数据，求得避雷针CD的长约为__m（结果精确到0.01 m）．（可用计算器求，也可用下列参考数据求：sin ≈0.682 0，sin 40°≈0.642 8，cos 43°≈0.731 4，cos 40°≈0.766 0，tan 43°≈0.932 5，tan 40°≈0.839 1）
 |
查看答案和解析>>
科目：初中数学 来源： 题型：
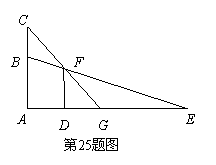
如图所示，一只猫头鹰蹲在一棵树AC的B（点B在AC上）处，发现一只老鼠躲进短墙DF的另一侧，猫头鹰的视线被短墙遮住.为了寻找这只老鼠猫头鹰向上飞至树顶C处.DF=4米，短墙底部D与树的底部A间的距离为2.7米，猫头鹰从C点观察F点的俯角为53°，老鼠躲藏处M (点M在DE上)距D点3米.（参考数据：sin 37°≈0.60, cos 37°≈0.80，tan 37°≈0.75）
(1)猫头鹰飞至C处后，能否看到这只老鼠？为什么？
(2)要捕捉到这只老鼠，猫头鹰至少要飞多少米（精确到0.1米
）？
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
解析：连接PP＇，过点B作BD⊥PP＇，交PP＇于点D，因为∠PBP＇=30°，所以∠PBD=15°，利用sin 15°=
，先求出PD，乘2即得PP＇.
中，
，
，BD是
的度数．
2倍 C.不变
D.不能确定
）
( )
B. 
C. 
D. 