
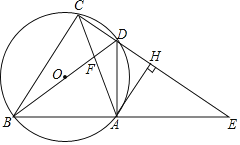
【题目】如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA交于点E,连接AC、BD交于点F,作AH⊥CE,垂足为点H,已知∠ADE=∠ACB.
(1)求证:AH是⊙O的切线;
(2)若OB=4,AC=6,求sin∠ACB的值;
(3)若![]() ,求证:CD=DH.
,求证:CD=DH.
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)连接OA,证明△DAB≌△DAE,得到AB=AE,得到OA是△BDE的中位线,根据三角形中位线定理、切线的判定定理证明;
(2)利用正弦的定义计算;
(3)证明△CDF∽△AOF,根据相似三角形的性质得到CD=![]() CE,根据等腰三角形的性质证明.
CE,根据等腰三角形的性质证明.
(1)证明:连接OA,
由圆周角定理得,∠ACB=∠ADB,
∵∠ADE=∠ACB,
∴∠ADE=∠ADB,
∵BD是直径,
∴∠DAB=∠DAE=90°,
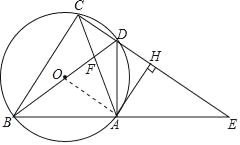
在△DAB和△DAE中,
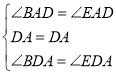 ,
,
∴△DAB≌△DAE,
∴AB=AE,又∵OB=OD,
∴OA∥DE,又∵AH⊥DE,
∴OA⊥AH,
∴AH是⊙O的切线;
(2)解:由(1)知,∠E=∠DBE,∠DBE=∠ACD,
∴∠E=∠ACD,
∴AE=AC=AB=6.
在Rt△ABD中,AB=6,BD=8,∠ADE=∠ACB,
∴sin∠ADB=![]() =
=![]() ,即sin∠ACB=
,即sin∠ACB=![]() ;
;
(3)证明:由(2)知,OA是△BDE的中位线,
∴OA∥DE,OA=![]() DE.
DE.
∴△CDF∽△AOF,
∴![]() =
=![]() ,
,
∴CD=![]() OA=
OA=![]() DE,即CD=
DE,即CD=![]() CE,
CE,
∵AC=AE,AH⊥CE,
∴CH=HE=![]() CE,
CE,
∴CD=![]() CH,
CH,
∴CD=DH.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
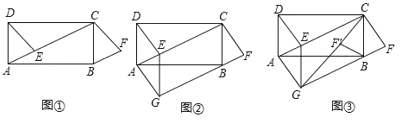
【题目】(操作)如图①,在矩形![]() 中,
中,![]() 为对角线
为对角线![]() 上一点(不与点
上一点(不与点![]() 重合),将
重合),将![]() 沿射线
沿射线![]() 方向平移到
方向平移到![]() 的位置,
的位置,![]() 的对应点为
的对应点为![]() .已知
.已知![]() (不需要证明).
(不需要证明).
(探究)过图①中的点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() ,其它条件不变,如图②.求证:
,其它条件不变,如图②.求证:![]() .
.
(拓展)将图②中的![]() 沿
沿![]() 翻折得到
翻折得到![]() ,连接
,连接![]() ,其它条件不变,如图③.当
,其它条件不变,如图③.当![]() 最短时,若
最短时,若![]() ,
,![]() ,直接写出
,直接写出![]() 的长和此时四边形
的长和此时四边形![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标.
【答案】(1)作图见解析;点A1的坐标(2,﹣4);(2)作图见解析;点A2的坐标(﹣2,4).
【解析】
试题分析:(1)分别找出A、B、C三点关于x轴的对称点,再顺次连接,然后根据图形写出A点坐标;
(2)将△A1B1C1中的各点A1、B1、C1绕原点O旋转180°后,得到相应的对应点A2、B2、C2,连接各对应点即得△A2B2C2.
试题解析:(1)如图所示:点A1的坐标(2,﹣4);
(2)如图所示,点A2的坐标(﹣2,4).
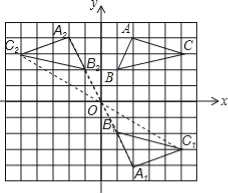
考点:1.作图-旋转变换;2.作图-轴对称变换.
【题型】解答题
【结束】
18
【题目】观察下面的点阵图和相应的等式,探究其中的规律:
(1)认真观察,并在④后面的横线上写出相应的等式.
![]()
①1=1 ②1+2=![]() =3 ③1+2+3=
=3 ③1+2+3=![]() =6 ④ …
=6 ④ …
(2)结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.
![]()
1=12②1+3=22③3+6=32④6+10=42⑤ …
(3)通过猜想,写出(2)中与第n个点阵相对应的等式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
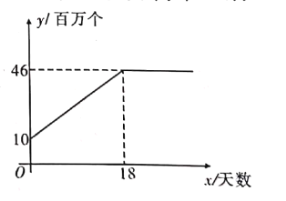
【题目】随着新冠肺炎的爆发,市场对口罩的需求量急剧增大.某口罩生产商自二月份以来,--直积极恢复产能,每日口罩生产量![]() (百万个)与天数
(百万个)与天数![]() 且
且![]() 为整数)的函数关系图象如图所示,而该生产商对口供应市场对口罩的需求量<(百万个)与天数
为整数)的函数关系图象如图所示,而该生产商对口供应市场对口罩的需求量<(百万个)与天数![]() 呈抛物线型,第
呈抛物线型,第![]() 天市场口罩缺口(需求量与供应量差)就达到
天市场口罩缺口(需求量与供应量差)就达到![]() (百万个),之后若干天,市场口罩需求量不断上升,在第
(百万个),之后若干天,市场口罩需求量不断上升,在第![]() 天需求量达到最高峰
天需求量达到最高峰![]() (百万个).
(百万个).
![]() 求出
求出![]() 与
与![]() 的函数解析式;
的函数解析式;
![]() 当市场供应量不小于需求量时,市民买口罩才无需提前预约,那么在整个二月份,市民无需预约即可购买口罩的天数共有多少天?
当市场供应量不小于需求量时,市民买口罩才无需提前预约,那么在整个二月份,市民无需预约即可购买口罩的天数共有多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
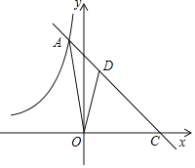
【题目】如图,在平面直角坐标系xOy中,函数y=﹣x+5的图象与函数y=![]() (k<0)的图象相交于点A,并与x轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
(k<0)的图象相交于点A,并与x轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
(1)求k的值;
(2)根据图象,直接写出当x<0时不等式![]() >﹣x+5的解集;
>﹣x+5的解集;
(3)求△AOD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
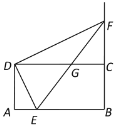
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 边上,与点
边上,与点![]() 、
、![]() 不重合,过点
不重合,过点![]() 作
作![]() 的垂线与
的垂线与![]() 的延长线相交于点
的延长线相交于点![]() ,连结
,连结![]() ,交
,交![]() 于点
于点![]() .
.
(1)当![]() 为
为![]() 的中点时,求
的中点时,求![]() 的长;
的长;
(2)当![]() 是以
是以![]() 为腰的等腰三角形时,求
为腰的等腰三角形时,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
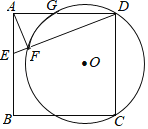
【题目】如图,正方形ABCD中,E为AB上一点,AF⊥DE于点F,已知DF=5EF=5,过C、D、F的⊙O与边AD交于点G,则DG=( )
A.2![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC=20,tanB=![]() ,点D为BC边上的动点(D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.
,点D为BC边上的动点(D不与点B,C重合).以D为顶点作∠ADE=∠B,射线DE交AC边于点E,过点A作AF⊥AD交射线DE于点F,连接CF.
(1)求证:△ABD∽△DCE;
(2)当DE∥AB时(如图2),求AE的长;
(3)点D在BC边上运动的过程中,是否存在某个位置,使得DF=CF?若存在,求出此时BD的长;若不存在,请说明理由.
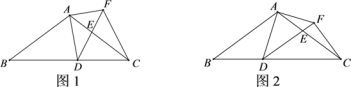
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com