[题目]已知一个正方体的体积是1000cm3 . 现在要在它的8个角上分别截去8个大小相同的小正方体.使截去后余下的体积是488cm3 . 问截得的每个小正方体的棱长是多少? 题目和参考答案——青夏教育精英家教网—

【题目】已知一个正方体的体积是1000cm3 ，现在要在它的8个角上分别截去8个大小相同的小正方体，使截去后余下的体积是488cm3 ，问截得的每个小正方体的棱长是多少？

【答案】解：设截得的每个小正方体的棱长xcm，依题意得
1000﹣8x3=488，
∴8x3=512，
∴x=4，
答：截得的每个小正方体的棱长是4cm
【解析】由于个正方体的体积是1000cm3 ，现在要在它的8个角上分别截去8个大小相同的小正方体，使截去后余下的体积是488cm3 ，设截得的每个小正方体的棱长xcm，根据已知条件可以列出方程1000﹣8x3=488，解方程即可求解．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，在由12个边长都为1且有一个锐角为60°的小菱形组成的网格中，点P是其中的一个顶点，以点P为直角顶点作格点直角三角形（即顶点均在格点上的三角形），请你写出所有可能的直角三角形斜边的长．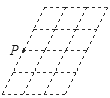

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图1，在平面直角坐标系中，A（a，0），B（b，0），C（﹣1，2），且|a+2|+（b﹣4）2=0.

（1）求a，b的值．
（2）在坐标轴上是否存在一点M，使△COM的面积= △ABC的面积，求出点M的坐标．
（3）如图2，过点C作CD⊥y轴交y轴于点D，点P为线段CD延长线上的一动点，连接OP，OE平分∠AOP，OF⊥OE．当点P运动时，的值是否会改变？若不变，求其值；若改变，说明理由．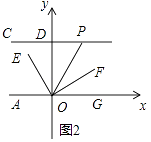

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】（1）画线段AC=30mm（点A在左侧）；
（2）以C为顶点，CA为一边，画∠ACM=90°；
（3）以A为顶点，AC为一边，在∠ACM的同侧画∠CAN=60°，AN与CM相交于点B；量得AB是多少mm？
（4）画出AB中点D，连接DC，此时量得DC是多少mm？请你猜想AB与DC的数量关系是：AB是DC的多少倍？
（5）作点D到直线BC的距离DE，且量得DE等于多少mm？请你猜想DE与AC的数量关系是：DE和AC的数量关系是？，位置关系是？．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】8月份是新学期开学准备季，东风和百惠两书店对学习用品和工具实施优惠销售．优惠方案分别是：在东风书店购买学习用品或工具书累计花费60元后，超出部分按50%收费；在百惠书店购买学习用品或工具书累计花费50元后，超出部分按60%收费，郝爱同学准备买价值300元的学习用品和工具书，她在哪家书店消费更优惠（）
A.东风
B.百惠
C.两家一样
D.不能确定

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】根据有关测定，当外界气温处于人体正常体温的黄金比值时，人体感到最舒适（人体正常体温约为37℃），这个气温大约为（）

A.23℃B.28℃C.30℃D.37℃

查看答案和解析>>

科目：初中数学 来源： 题型：

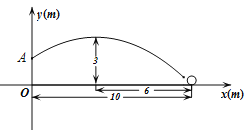
【题目】如图，在某场足球比赛中，球员甲从球门底部中心点O的正前方10m处起脚射门，足球沿抛物线飞向球门中心线；当足球飞离地面高度为3m时达到最高点，此时足球飞行的水平距离为6m．已知球门的横梁高为2.44m．

（1）在如图所示的平面直角坐标系中，问此飞行足球能否进球门？（不计其它情况）

（2）守门员乙站在距离球门2m处，他跳起时手的最大摸高为2.52m，他能阻止球员甲的此次射门吗？如果不能，他至少后退多远才能阻止球员甲的射门？