
【题目】如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°. 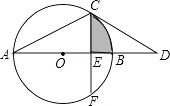
(1)求∠A的度数;
(2)若点F在⊙O上,CF⊥AB,垂足为E,CF= ![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】
(1)解:连接OC,
∵CD切⊙O于点C
∴∠OCD=90°
∵∠D=30°
∴∠COD=60°
∵OA=OC
∴∠A=∠ACO=30°
(2)解:∵CF⊥直径AB,CF= ![]()
∴CE= ![]()
∴在Rt△OCE中,tan∠COE= ![]() ,
,
OE= ![]() =
= ![]() =2,
=2,
∴OC=2OE=4
∴S扇形BOC= ![]() ,
, ![]()
∴S阴影=S扇形BOC﹣S△EOC= ![]() .
.
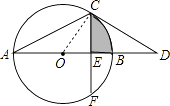
【解析】(1)连接OC,则△OCD是直角三角形,可求出∠COD的度数;由于∠A与∠COD是同弧所对的圆周角与圆心角.根据圆周角定理即可求得∠A的度数;(2)由图可知:阴影部分的面积是扇形OCB和Rt△OEC的面积差;那么解决问题的关键是求出半径和OE的长;在Rt△OCE中,∠OCE=∠D=30°,已知了CE的长,通过解直角三角形,即可求出OC、OE的长,由此得解.
【考点精析】利用切线的性质定理和扇形面积计算公式对题目进行判断即可得到答案,需要熟知切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣x2﹣2x+3与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)请直接写出点A,C,D的坐标;
(2)如图(1),在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;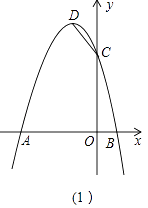
(3)如图(2),F为直线AC上的动点,在抛物线上是否存在点P,使得△AFP为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.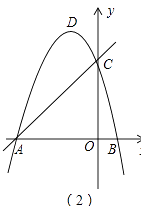
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校部分学生选择社团的意向,并将调查结果绘制成如下统计图(不完整):
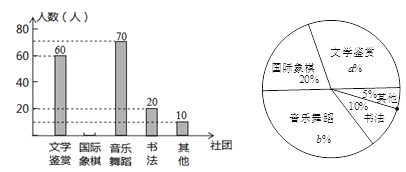
根据统计图的信息,解答下列问题:
(1)求本次抽样调查的学生总人数及a、b的值;
(2)将条形统计图补充完整;
(3)若该校共有1300名学生,试估计全校选择“音乐舞蹈”社团的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为切实减轻中小学生课业负担、全面实施素质教育,某中学对本校学生课业负担情况进行调查.在本校随机抽取若干名学生进行问卷调查,发现被抽查的学生中,每天完成课外作业时间,最长不足120分钟,没有低于40分钟的,且完成课外作业时间低于60分钟的学生数占被调查人数的10%.现将抽查结果绘制成了一个不完整的频数分布直方图,如图所示. 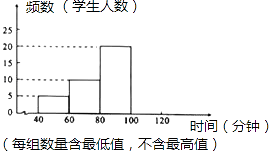
(1)这次被抽查的学生有人;
(2)请补全频数分布直方图;
(3)被调查这些学生每天完成课外作业时间的中位数在组(填时间范围);
(4)若该校共有3600名学生,请估计该校大约有多少名学生每天完成课外作业时间在80分钟以上(包括80分钟).
查看答案和解析>>
科目:初中数学 来源: 题型:
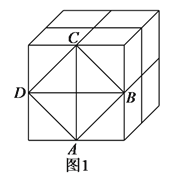
【题目】如图1,这是由8个同样大小的立方体组成的魔方,体积为64.
(1)求出这个魔方的棱长.
(2)图中阴影部分是一个正方形![]() ,求出阴影部分的面积及其边长.
,求出阴影部分的面积及其边长.
(3)把正方形![]() 放到数轴上,如图
放到数轴上,如图![]() ,使得
,使得![]() 与
与![]() 重合,点
重合,点![]() 与
与![]() 重合,点
重合,点![]() 与点
与点![]() 关于
关于![]() 点对称,那么
点对称,那么![]() 在数轴上表示的数为__________;点
在数轴上表示的数为__________;点![]() 在数轴上表示的数为__________.
在数轴上表示的数为__________.
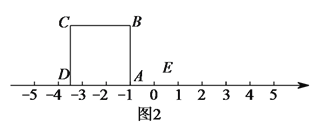
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com