
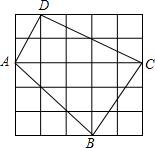
 如图,每个小方格的边长都为1.
如图,每个小方格的边长都为1.分析 (1)连接AC,四边形可以把它看成两个三角形,即△ADC,△ABC,再求出其面积的和即可;
(2)可求得AC、CD、AD的长,利用勾股定理的逆定理可判定AD、CD的位置关系.
解答 解:(1)∵S△ADC=5×2÷2=5,S△ABC=5×3÷2=7.5,
∴四边形ABCD的面积=S△ADC+S△ABC=5+7.5=12.5;
(2)由勾股定理,得AD=$\sqrt{5}$,CD=2$\sqrt{5}$,
由题意可知AC=5,
∴AD2+CD2=($\sqrt{5}$)2+(2$\sqrt{5}$)2=25=AC2,
∴△ACD为直角三角形,
∴∠ADC=90°,
∴AD⊥CD.
点评 本题主要考查了三角形的面积以及勾股定理及其逆定理的应用,掌握勾股定理求边长及由三边之间的平方关系判定直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
| 甲组 | 6.7 | 6 | 3.4 | 90% | 20% |
| 乙组 | 7.1 | 7.5 | 1.69 | 80% | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是某农场大棚里三种蔬菜种植面积的扇形统计图,根据所给数据填空
如图是某农场大棚里三种蔬菜种植面积的扇形统计图,根据所给数据填空查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com