
(本小题满分5分)已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于点D、E,联结EB交OD于点F.
(1)求证:OD⊥BE;
(2)若DE= ,AB=5,求AE的长.
,AB=5,求AE的长.
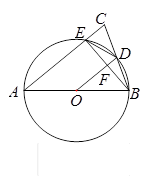
解:(1)联结AD
∵AB是⊙O的直径,∴∠ADB=∠AEB =90° --- 1分
∵AB=AC,∴CD=BD
∵OA=OB,∴OD//AC
∴OD⊥BE ------------------------------------------------------------- 2分
(2)方法一:∵∠CEB=∠AEB=90°,CD=BD,AB=5, DE=
∴AC=AB=5, BC=2DE=2![]() , ------------------------------------ 3分
, ------------------------------------ 3分
在△ABE、△BCE中,∠CEB=∠AEB=90°,则有![]()
设AE=x, 则![]() --------------------------------- 4分
--------------------------------- 4分
解得:x=3
∴AE=3 ----------------------------------------------5分
方法二:∵OD⊥BE,∴BD=DE,BF=EF -----------------------------------3分
设AE=x,∴OF=![]() ,在△OBF、△BDF中,∠OFB=∠BFD=90°
,在△OBF、△BDF中,∠OFB=∠BFD=90°
∴![]()
∵DE=![]() ,AB=5,
,AB=5,
∴![]() --------------------4分
--------------------4分
解得:x=3, ∴AE=3 ----------------------------5分
方法三:∵BE⊥AC AD⊥BC,
∴S△ABC= BC·AD=
BC·AD=![]() AC·BE, -------------------------------------------3分
AC·BE, -------------------------------------------3分
∴BC·AD=AC·BE
∵BC=2DE=2![]() ,AC=AB=5
,AC=AB=5
∴BE=4, -------------------------------------------4分
∴AE=3 --------------------------------------------5分
解析:略


科目:初中数学 来源: 题型:

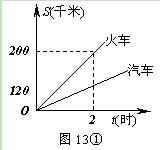
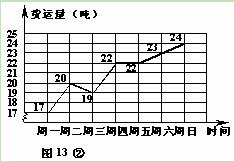
查看答案和解析>>
科目:初中数学 来源: 题型:
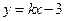 经过点M(2,1),且与x轴交于点A,与y轴交于点B.
经过点M(2,1),且与x轴交于点A,与y轴交于点B.
查看答案和解析>>
科目:初中数学 来源: 题型:
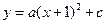 与y轴交于点C(0,
与y轴交于点C(0,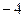 ), 与x轴交于点A、 B,点A的坐标为(2,0).
), 与x轴交于点A、 B,点A的坐标为(2,0).
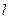 与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(
与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(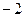 ,0).问:是否存在这样的直线
,0).问:是否存在这样的直线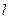 ,使得△OMF是等腰三角形?若存 在,请求出点Q的坐标;若不存在,请说明理由.
,使得△OMF是等腰三角形?若存 在,请求出点Q的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:2010-2011学年河南省周口市初三下学期第二十七章相似三角形检测题 题型:解答题
(本小题满分7分)
已知:关于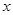 的一元二次方程
的一元二次方程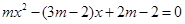 .
.
(1)若方程有两个不相等的实数根,求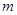 的取值范围;
的取值范围;
(2)在(1)的条件下,求证:无论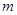 取何值,抛物线y=
取何值,抛物线y=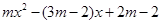 总过
总过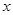 轴上的一个固定点;
轴上的一个固定点;
(3)若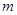 为正整数,且关于
为正整数,且关于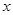 的一元二次方程
的一元二次方程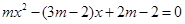 有两个不相等的整数根,把抛物线y=
有两个不相等的整数根,把抛物线y=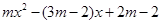 向右平移4个单位长度,求平移后的抛物线的解析式.
向右平移4个单位长度,求平移后的抛物线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com