
����Ŀ����ƽ��ֱ������ϵ�У�A(6��a)��B(b��0)��M(0��c)��P��Ϊy����һ���㣬��(b��2)2+|a��6|+![]() ��0��
��0��
(1)���B��M�����ꣻ
(2)��P�����߶�OM���˶�ʱ�������Ƿ����һ����PʹS��PAB��13�������ڣ������P���������AB�ij��ȣ��������ڣ���˵�����ɣ�
(3)����P���˶���ֱ��OM�ϵ��κ�λ��(��������O��M)����PAM����APB����PBO����֮���Ƿ���ij�̶ֹ���������ϵ������У���������ѧ֪ʶ�ҳ���֤�������û�У���˵�����ɣ�
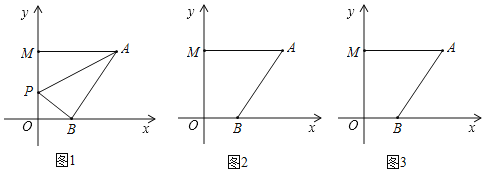
���𰸡���1��M��0��6����B��2��0����A��6��6������2��AB=2![]() ����3���ٵ���P���߶�OM��ʱ�����ۣ���APB+��PBO=��PAM�����ɼ��������ڵ���P��MO���ӳ�����ʱ�����ۣ���APB+��PBO=��PAM�����ɼ��������۵���P��OM���ӳ�����ʱ�����ۣ���PBO=��PAM+��APB�����ɼ�������
����3���ٵ���P���߶�OM��ʱ�����ۣ���APB+��PBO=��PAM�����ɼ��������ڵ���P��MO���ӳ�����ʱ�����ۣ���APB+��PBO=��PAM�����ɼ��������۵���P��OM���ӳ�����ʱ�����ۣ���PBO=��PAM+��APB�����ɼ�������
��������
��1�����÷Ǹ��������ʣ����a��b��c���ɽ�����⣻
��2����P��0��m��������S��PAB=S����AMOB-S��APM-S��PBO���������̼��ɽ�����⣻
��3�����������Σ��ֱ�ͼ�ν�����⼴����
��1���ߣ�b-2��2+|a-6|+![]() =0��
=0��
���ߣ�b-2��2����0��|a-6|��0��![]() ��0��
��0��
��a=6��b=2��c=6��
��M��0��6����B��2��0����A��6��6����
��2����P��0��m����
��S��PAB=13���ı���AMOB��ֱ�����Σ�
��![]() ��6+2��6-
��6+2��6-![]() m2-
m2-![]() ��6-m��6=13��
��6-m��6=13��
��m=![]() ��
��
��P��0��![]() ����
����
AB=![]() =2
=2![]() ��
��
��3������ͼ2-1�У�����P���߶�OM��ʱ�����ۣ���APB+��PBO=��PAM��
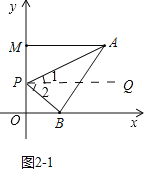
���ɣ���PQ��AM����PQ��AM��ON��
���1=��PAM����2=��PBO��
���1+��2=��PAM+��PBO��
����APB=��PAM+��PBO��
��APB+��PBO=��PAM��
����ͼ2-2����ʾ������P��MO���ӳ�����ʱ�����ۣ���APB+��PBO=��PAM��
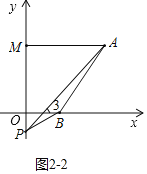
���ɣ���AM��OB��
���PAM=��3��
�ߡ�3=��APB+��PBO��
���APB+��PBO=��PAM��
����ͼ2-3�У�����P��OM���ӳ�����ʱ�����ۣ���PBO=��PAM+��APB��
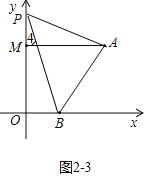
���ɣ���AM��OB��
���4=��PBO��
�ߡ�4=��PAM+��APB��
���PBO=��PAM+��APB��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ɼ�����ͬ��С�������ɵļ����壬
��1����������������Ҫ���� ��������С�����壻
��2��������������������ͼ������ͼ��
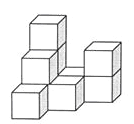
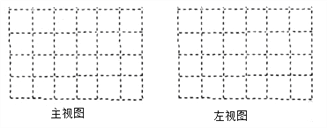
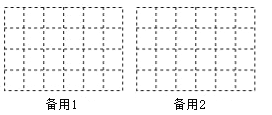
��3���ڱ�������ͼ������ͼ���������£��������õ�n��С�����壬��n=�� �����������ڱ���ͼ�л����õ�n��С��������µļ�����ĸ���ͼ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C1��y=x2+2x��3��x�ύ�ڵ�A��B����A�ڵ�B��ࣩ����y�ύ�ڵ�C��������C2��y=ax2+bx+c������B����x�����һ������ΪE����4��0������y�ύ�ڵ�D��0��2����
��1����������C2�Ľ���ʽ��
��2�����PΪ�߶�AB��һ���㣨��P�����A��B�غϣ�������P��x��Ĵ��߽�������C1�ڵ�M����������C2�ڵ�N��
�ٵ��ı���AMBN��������ʱ�����P�����ꣻ
�ڵ�CM=DN��0ʱ�����P�����꣮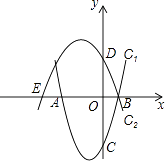
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
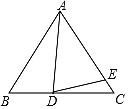
����Ŀ����ͼ��ʾ����֪�ڡ�ABC�У�AB��AC��DΪ�߶�BC��һ�㣬EΪ�߶�AC��һ�㣬��AD��AE��
(1)����ABC��60�㣬��ADE��70�㣬���BAD���CDE�Ķ�����
(2)���BAD��������CDE��������д��������֮��Ĺ�ϵ������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=2x2��x��3��
��1������ͼ��Ķ������꣬�������ύ�����꣬��������������ͼ�� 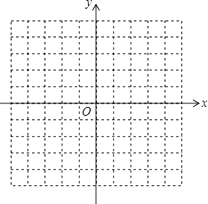
��2������ͼ��ֱ�ӻش𣺵�xΪ��ֵʱ��y��0����xΪ��ֵʱy����3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼA������������Ӧ����Ϊ��2��
��1����B�ڵ�A�ұ߾�A��4����λ���ȣ����B����Ӧ������
��2���ڣ�1���������£���A��ÿ��2����λ���������������˶����� B ��ÿ��2����λ���������������˶�������A�˶�����6���ڵĵ㴦ʱ����A��B�������룮
��3������2���������£���A�㾲ֹ������B������ÿ��2����λ���������������˶�ʱ�������ʱ��A��B�������4����λ���ȣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
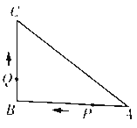
����Ŀ����ͼ����֪��ABC�У���B=90�㣬AB=8 cm��BC=6 cm��P��Q�ǡ�ABC���ϵ��������㣬��P�ӵ�A��ʼ��A��B�����˶������ٶ�Ϊ1 cm����Q�ӵ�B��ʼ��B��C�����˶������ٶ�Ϊ2 cm/s������ͬʱ���������˶���ʱ��Ϊt s.
��1���˶�����ʱ����APC�ǵ��������Σ�
��2������Q�ڱ�CA���˶�ʱ������ʹ��BCQ��Ϊ���������ε��˶�ʱ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ���ر������������(��ͼ)�������Ϲ����������ĵ���֮������7�������ķ�ͼ�п����۳ɷ��Ϲ�������ӵ���(����)��
![]()
A. 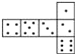 B.
B. 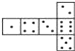 C.
C.  D.
D. 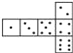
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=��![]() x+8��x�ᡢy��ֱ��ཻ�ڵ�A��B����M��OB��һ�㣬������ABM��AM�۵���ʹ��Bǡ������x���ϵĵ�B�䴦����
x+8��x�ᡢy��ֱ��ཻ�ڵ�A��B����M��OB��һ�㣬������ABM��AM�۵���ʹ��Bǡ������x���ϵĵ�B�䴦����
��1����B������ꣻ
��2��ֱ��AM����Ӧ�ĺ�����ϵʽ��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com