
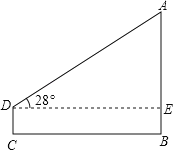
【题目】某数学课外活动小组的同学.利用所学的数学知识,测底部可以到达的学校操场上的旗杆AB高度,他们采用了如下两种方法:
方法1:在地面上选一点C,测得CB为40米,用高为1.6米的测角仪在C处测得旗杆顶部A的仰角为28°;
方法2:在相同时刻测得旗杆AB的影长为17.15米,又测得已有的2米高的竹杆的影长为1.5米.
你认为这两种方法可行吗?若可行,请你任选一种方法算出旗杆高度(精确到0.1米)若不可行,自己另设计一种测量方法(旗杆顶端不能到达),算出旗杆高度(结果可用字母表示)
科目:初中数学 来源: 题型:
【题目】端午节放假期间,小明和小华准备到宜宾的蜀南竹海(记为A)、兴文石海(记为B)、夕佳山民居(记为C)、李庄古镇(记为D)的一个景点去游玩,他们各自在这四个景点中任选一个,每个景点都被选中的可能性相同.
(1)小明选择去蜀南竹海旅游的概率为 .
(2)用树状图或列表的方法求小明和小华都选择去兴文石海旅游的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(-4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
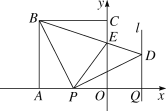
(1)∠PBD的度数为 ,点D的坐标为 (用t表示);
(2)当t为何值时,△PBE为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程.
已知:直线![]() 和直线外一点
和直线外一点![]() .
.
求作:直线![]() 的垂线,使它经过
的垂线,使它经过![]() .
.
作法:如图2.
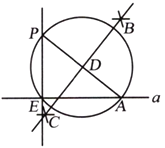
(1)在直线![]() 上取一点
上取一点![]() ,连接
,连接![]() ;
;
(2)分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧相交于
的长为半径作弧,两弧相交于![]() ,
,![]() 两点,连接
两点,连接![]() 交
交![]() 于点
于点![]() ;
;
(3)以点![]() 为圆心,
为圆心,![]() 为半径作圆,交直线
为半径作圆,交直线![]() 于点
于点![]() (异于点
(异于点![]() ),作直线
),作直线![]() .所以直线
.所以直线![]() 就是所求作的垂线.
就是所求作的垂线.
请你写出上述作垂线的依据:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为2的正方形![]() 在平面直角坐标系中的位置如图所示,点
在平面直角坐标系中的位置如图所示,点![]() 是边
是边![]() 的中点,连接
的中点,连接![]() ,点
,点![]() 在第一象限,且
在第一象限,且![]() ,
,![]() .以直线
.以直线![]() 为对称轴的抛物线过
为对称轴的抛物线过![]() ,
,![]() 两点.
两点.

(1)求抛物线的解析式;
(2)点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 每秒1个单位长度的速度运动,运动时间为
每秒1个单位长度的速度运动,运动时间为![]() 秒.过点
秒.过点![]() 作
作![]() 于点
于点![]() ,当
,当![]() 为何值时,以点
为何值时,以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?
相似?
(3)点![]() 为直线
为直线![]() 上一动点,点
上一动点,点![]() 为抛物线上一动点,是否存在点
为抛物线上一动点,是否存在点![]() ,
,![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.
为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,长方形ABCD(每个内角都是90°)的顶点的坐标分别是A(0,m),B(n,0),(m>n>0),点E在AD上,AE=AB,点F在y轴上,OF=OB,BF的延长线与DA的延长线交于点M,EF与AB交于点N.
(1)试求点E的坐标(用含m,n的式子表示);
(2)求证:AM=AN;
(3)若AB=CD=12cm,BC=20cm,动点P从B出发,以2cm/s的速度沿BC向C运动的同时,动点Q从C出发,以vcm/s的速度沿CD向D运动,是否存在这样的v值,使得△ABP与△PQC全等?若存在,请求出v值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东坡商贸公司购进某种水果成本为20元/![]() ,经过市场调研发现,这种水果在未来48天的销售单价
,经过市场调研发现,这种水果在未来48天的销售单价![]() (元/
(元/![]() )与时间
)与时间![]() (天)之间的函数关系式
(天)之间的函数关系式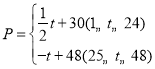 ,
,![]() 为整数,且其日销售量
为整数,且其日销售量![]() (
(![]() )与时间
)与时间![]() (天)的关系如下表:
(天)的关系如下表:
时间 | 1 | 3 | 6 | 10 | 20 | … |
日销售量 | 118 | 114 | 108 | 100 | 80 | … |
(1)已知![]() 与
与![]() 之间的变化符合一次函数关系,试求在第30天的日销售量;
之间的变化符合一次函数关系,试求在第30天的日销售量;
(2)哪一天的销售利润最大?最大日销售利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以边长为8的正方形纸片ABCD的边AB为直径作⊙O,交对角线AC于点E.
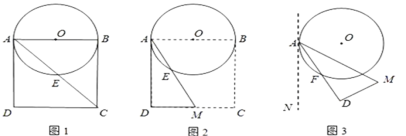
(1)线段AE= ;
(2)如图2,以点A为端点作∠DAM=30°,交CD于点M,沿AM将四边形ABCM剪掉,使Rt△ADM绕点A逆时针旋转(如图3),设旋转角为α(0°<α<150°),旋转过程中AD与⊙O交于点F.
①当α=30°时,请求出线段AF的长;
②当α=60°时,求出线段AF的长;判断此时DM与⊙O的位置关系,并说明理由;
③当α= °时,DM与⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AC为对角线,延长CD至点E使CE=CA,连接AE.F为AB上的一点,且BF=DE,连接FC.
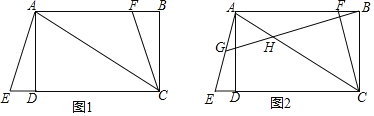
(1)若DE=1,CF=![]() ,求CD的长;
,求CD的长;
(2)如图2,点G为线段AE的中点,连接BG交AC于H,若∠BHC+∠ABG=60°,求证:AF+CE=![]() AC.
AC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com