
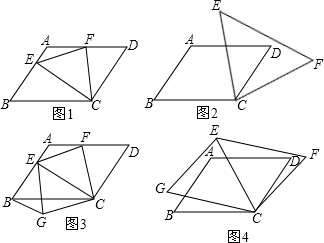
���� ��Ȳ��룺����AC�������ı���ABCD�����Σ���B=60�㣬�ó���EAF=60�㣬AD=CD=AB����ADC=��B=60�㣬��ô��ACD�ǵȱ������Σ�����AC=DC����ACD=��CAD=60�㣬�ٸ���SAS֤����ACE�ա�DCF���õ�CE=CF����ACE=��DCF��Ȼ�������ECF=��ACD=60�㣬���ǵó���CEF�ǵȱ������Σ�
�����о�����1������AC������SAS֤����BCG�ա�ACE���ó�BG=AE����AF=BE�����ǵó�AF+BG=AB��
��2��ͬ��1��������AC������SAS֤����BCG�ա�ACE���ó�BG=AE����AF=BE�����ǵó���1���еĽ��۲��������µĽ���ΪAF-BG=AB��
��� 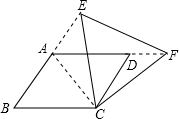 �⣺��Ȳ��룺��CEF��ȻΪ�ȱ������Σ��������£�
�⣺��Ȳ��룺��CEF��ȻΪ�ȱ������Σ��������£�
����AC��
���ı���ABCD�����Σ���B=60�㣬
���EAF=60�㣬AD=CD=AB����ADC=��B=60�㣬
���ACD�ǵȱ������Σ�
��AC=DC����ACD=��CAD=60�㣬
���CAE=��CDF=120�㣬
��BE=AF��
��BE-AB=AF-AD����AE=DF��
���ACE�ա�DCF��
��CE=CF����ACE=��DCF��
���DCF+��DCE=��ACE+��DCE������ECF=��ACD=60�㣬
���CEF�ǵȱ������Σ�
�����о��� ��1��AF+BG=AB���������£�
��1��AF+BG=AB���������£�
����AC���á�BCA=60�㣮
��EG��CF��EG=CF��
���ı���CFEG��ƽ���ı��Σ�
��EF=GC��
�ߡ�CEF�ǵȱ������Σ�
��EF=CE=CF��
��CE=CG=EG��
���CEG�ǵȱ������Σ�
���GCE=60�㣬
���GCE-��BCE=��BCA-��BCE������GCB=��ECA��
���BCG�ա�ACE��SAS����
��BG=AE��
��AF=BE��
��AF+BG=BE+AE����AF+BG=AB��
��2����1���еĽ��۲��������µĽ���ΪAF-BG=AB��
���� �������ı����ۺ��⣬�����漰�����ε����ʣ��ȱ������Ρ�ȫ�������Ρ�ƽ���ı��ε��ж������ʣ��ۺ��Խ�ǿ���Ѷ����У��������ν�ϼ����˼���ǽ���Ĺؼ���


 ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������ABCD�ĶԽ���AC��BD���ڵ�O����AD=6��AB=8��E��F�ֱ���OD��CD���е㣬���DEF�����Ϊ3��
��ͼ������ABCD�ĶԽ���AC��BD���ڵ�O����AD=6��AB=8��E��F�ֱ���OD��CD���е㣬���DEF�����Ϊ3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��A | B�� | ��B | C�� | ��C | D�� | ��D |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
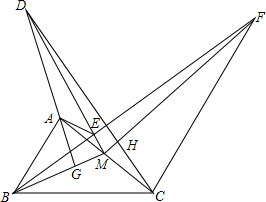 ��G�ǡ�ABC�����ģ�M�DZ�AC���е㣬��AC=2$\sqrt{3}$GM��D��GA�ӳ�������һ�㣬����DM������DM��ȡһ��E��ʹ��AED=��CAG����CF��AB��ֱ��BE���ڵ�F��CD��MF���ڵ�H����֤��
��G�ǡ�ABC�����ģ�M�DZ�AC���е㣬��AC=2$\sqrt{3}$GM��D��GA�ӳ�������һ�㣬����DM������DM��ȡһ��E��ʹ��AED=��CAG����CF��AB��ֱ��BE���ڵ�F��CD��MF���ڵ�H����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com