

���� ��1����P��PQ��CA��AB��G����BF��Q�����ݡ�BPE=$\frac{1}{2}$��BCA��֪��BPE=$\frac{1}{2}$��BCA=$\frac{1}{2}$��BPQ���ٸ���BD��PE���ɵá�BPQ�ǵ��������Σ�����BD=$\frac{1}{2}$BQ����ȫ�������ε��ж�������֪��BGQ�ա�PGE������PE=BQ���ʿɵó����ۣ�
��3��ͬ��2���ɵá�BGQ�ס�PGE������$\frac{BQ}{PE}$=$\frac{BG}{PG}$=$\frac{AB}{AC}$=m������BD=$\frac{1}{2}$BQ���ɵó����ۣ�
��� �⣺��1��PE=2BD���������£�
��ͼ�ڣ�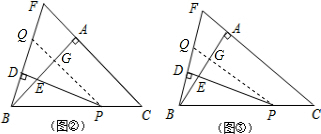
��P��PQ��CA��AB��G����BF��Q��
�ߡ�BPE=$\frac{1}{2}$��BCA��
���BPE=$\frac{1}{2}$��BCA=$\frac{1}{2}$��BPQ��
��BD��PE��
���BPQ�ǵ��������Σ�
��BD=$\frac{1}{2}$BQ��
��PQ��AC��BA��AC��
��BA��PQ��
��AB=AC��
��PG=BG��
�ߡ�DBE+��DEB=90�㣬��DEB=��GEP����GEP+��GPE=90�㣬
���DBE=��GPE��
�ڡ�BGQ���PGE�У�
$\left\{\begin{array}{l}{��PGE=��BGQ}\\{PG=BG}\\{��GPE=��DBE}\end{array}\right.$��
���BGQ�ա�PGE��ASA����
��PE=BQ��
��$\frac{BD}{PE}$=$\frac{1}{2}$��
��PE=2BD
��2���⣺��ͼ�ۣ�
��ͬ��1���ɵá�BGQ�ס�PGE��
��$\frac{BQ}{PE}$=$\frac{BG}{PG}$=$\frac{AB}{AC}$=m��
��BD=$\frac{1}{2}$BQ��
��$\frac{BD}{PE}$=$\frac{1}{2}$m
��$\frac{PE}{BD}$=$\frac{2}{m}$��
���� ���⿼��������������ε��ж������ʣ��漰��ȫ�������ε��ж������ʡ����������ε��ж������ʡ��������������ߺ�һ�����ʵ�֪ʶ���Ѷ����У�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
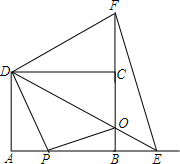 ��ͼ������ABCD�У�����P�ӵ�A���������߶�AB��ÿ��2cm���ٶ����B�˶���ͬʱ����Q�ӵ�B���������߶�BC��ÿ��1cm���ٶ����C�˶�������P����B��ʱ����Qͬʱֹͣ�����˶�ʱ��Ϊt�룮��֪AD=6����t=2ʱ��PQ=2$\sqrt{5}$��
��ͼ������ABCD�У�����P�ӵ�A���������߶�AB��ÿ��2cm���ٶ����B�˶���ͬʱ����Q�ӵ�B���������߶�BC��ÿ��1cm���ٶ����C�˶�������P����B��ʱ����Qͬʱֹͣ�����˶�ʱ��Ϊt�룮��֪AD=6����t=2ʱ��PQ=2$\sqrt{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
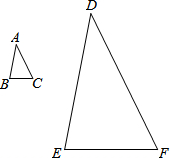 ��ͼ����ABC�ס�DEF��AB��DE=1��4����ô����Ҫ16����ABC���ܽ���DEF��Ƕ����
��ͼ����ABC�ס�DEF��AB��DE=1��4����ô����Ҫ16����ABC���ܽ���DEF��Ƕ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
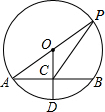 ��ͼ����O�İ뾶OD����AB�ڵ�C������AO���ӳ�����O�ڵ�P������PC����AB=8��OC=3����PC=2$\sqrt{13}$��
��ͼ����O�İ뾶OD����AB�ڵ�C������AO���ӳ�����O�ڵ�P������PC����AB=8��OC=3����PC=2$\sqrt{13}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
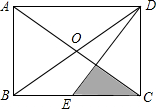 ��ͼ��������ABCD�У�����BD��AC����O��E��BC���е㣬��Ӱ���ֵ������6ƽ�����ף�����ABCD�������
��ͼ��������ABCD�У�����BD��AC����O��E��BC���е㣬��Ӱ���ֵ������6ƽ�����ף�����ABCD��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
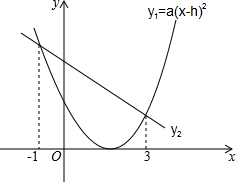 ��ͼ������˵����ȷ���ǣ�������
��ͼ������˵����ȷ���ǣ�������| A�� | ��y1��y2ʱ���Ա���x��ȡֵ��Χ����ȷ�� | |
| B�� | ��y1��y2ʱ��-1��x��3 | |
| C�� | ��y1��y2ʱ��-1��x��3 | |
| D�� | ��y1��y2ʱ��x��-1��x��3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com