


 );
);
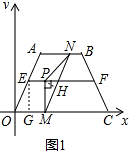
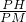 ,所以PH=PM•sin30°=
,所以PH=PM•sin30°=
 PH•MN=
PH•MN= ×4×
×4× =
= ,
,
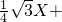
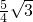 ,
, ,
,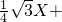
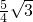
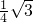 <0,
<0, ;
;
 ×(2+3)×
×(2+3)× =
=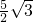 (如图1),
(如图1), (E′H′+D′G′)•D′E′=
(E′H′+D′G′)•D′E′= ×(4-t+5-t)×
×(4-t+5-t)× =-
=- t+
t+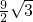 ,
, (5-t)
(5-t) DC•DE=(5-t)×
DC•DE=(5-t)× ×
× (5-t)=
(5-t)=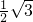 (5-t)2.
(5-t)2.

 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
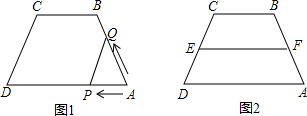 条件时,其一定平分梯形的面积?(只要求说出条件,不需证明)
条件时,其一定平分梯形的面积?(只要求说出条件,不需证明)查看答案和解析>>
科目:初中数学 来源: 题型:
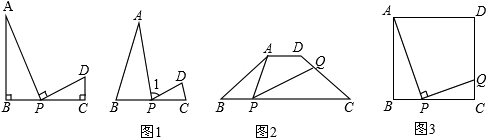
查看答案和解析>>
科目:初中数学 来源: 题型:
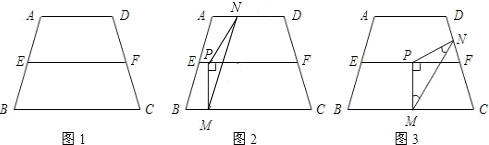
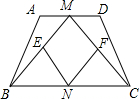 (2009•黔南州)杨老师在上四边形时给学生出了这样一个题.如图,若在等腰梯形ABCD中,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点时.提出以下问题:
(2009•黔南州)杨老师在上四边形时给学生出了这样一个题.如图,若在等腰梯形ABCD中,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点时.提出以下问题:查看答案和解析>>
科目:初中数学 来源: 题型:
| k | x |
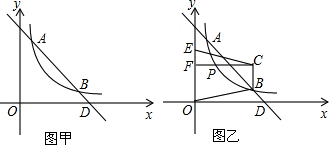
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com