练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
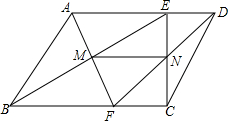
    14．如图，在平行四边形ABCD中，E，F分别是AD，BC上的点，且AE=BF，BE交AF于M，CE交DF于N，求证：MN$\stackrel{∥}{=}$$\frac{1}{2}$AD．

    分析 证明△AEM≌△FMB即可证明AM=MF，同理DN=NF，即MN是△ADF的中位线，根据三角形中位线定理证得．

    解答 证明：∵平行四边形ABCD中，AD∥BC．
    ∴∠DAF=∠AFB，
    ∴在△AEM和△FMB中，$\left\{\begin{array}{l}{∠DAM=∠AFB}\\{∠AME=∠FMB}\\{AE=BF}\end{array}\right.$，
    ∴△AEM≌△FMB，
    ∴AM=MF，
    同理，DN=NF，
    ∴MN是△ADF的中位线，
    ∴MN$\stackrel{∥}{=}$$\frac{1}{2}$AD．

    点评 本题考查了三角形的中位线定理，三角形的中位线平行于第三边且等于第三边的一半．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    4．若实数a满足a2+a=1，则-2a2-2a+2015=2013．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

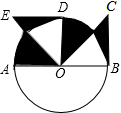    5．如图，AB是⊙O的直径，过点B作BC⊥OB，且BC=OB，点C在AB的上方，连接OC，△OBC绕着点O逆时针旋转90°得到△ODE
    （1）求证：DE是⊙O的切线；
    （2）若AB=8，求图中阴影部分的面积和．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如果反比例函数y=$\frac{{k}^{2}+1}{x}$的图象经过点A（x1，y1），B（x2，y2），C（x3，y3）且x1＞x2＞0＞x3，请比较y1、y2、y3的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．解不等式组：$\left\{\begin{array}{l}{\frac{2x-1}{3}≥-1}\\{\frac{2x-1}{3}＜6}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知方程$\frac{x-1}{x-2}$-$\frac{x-2}{x+1}$=$\frac{2x+a}{（x-2）（x+1）}$．
    （1）当a为何值时，此方程无解；
    （2）当a为何值时，此方程有解；
    （3）当a为何值时，此方程的解为正数？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．某水果店总共筹备了5.1万资金计划购入一些时令水果销售（品种及价格如下表所示）．现租用一辆载货量2.4吨的小货车进货（租金600元），要求将余下资金全部用于采购水果并使得所购水果装满货车．问应该怎样安排进货才能使水果店在销售完这批水果后获利最多？此时最大销售利润为多少元？
    水果名称进货价（元/千克）销售价（元/千克）
    凤梨1019
    芒果2636
    荔枝2230

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．下列各实数中，最小的是（　　）
    A．-πB．（-1）0C．$\root{3}{-1}$D．|-2|

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图，由边长为1的小正方形组成的网格中，A、B、C三点都在网格的格点上．则tan∠BAC=$\frac{1}{2}$．

    查看答案和解析>>

    同步练习册答案