
【题目】综合与实践
在数学活动课上,老师给出如下问题,让同学们展开探究活动:
[问题情境]
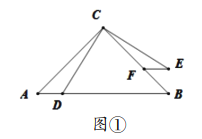
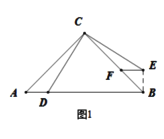
如图①,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 上一点
上一点![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到的对应线段为
,得到的对应线段为![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,请你根据上述条件,提出恰当的数学问题并解答.
,请你根据上述条件,提出恰当的数学问题并解答.
[解决问题]
下面是学习小组提出的三个问题,请你解答这些问题:
(1)“兴趣”组提出的问题是:求证:![]() ;
;
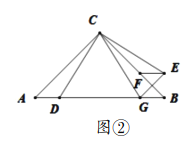
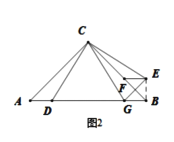
(2)“实践”小组提出的问题是:如图②,若将![]() 沿
沿![]() 的垂直平分线对折,得到
的垂直平分线对折,得到![]() ,连接
,连接![]() ,则线段
,则线段![]() 与
与![]() 有怎样的数量关系?请说明理由;
有怎样的数量关系?请说明理由;
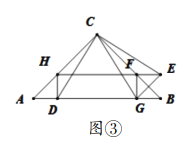
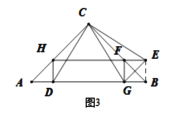
(3)“奋进”小组在“实践”小组探究的基础上,提出了如下问题:延长![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,求证:四边形
,求证:四边形![]() 是矩形.
是矩形.
【答案】(1)见解析;(2)![]() ,理由见解析;(3)见解析.
,理由见解析;(3)见解析.
【解析】
(1)连接![]() ,证明
,证明![]() ,得到AD=BE,
,得到AD=BE,![]() ,证出∠ABE=90°,由平行线的性质得出∠FEB=90°,得出
,证出∠ABE=90°,由平行线的性质得出∠FEB=90°,得出![]() ,证出EF=BE,即可得出结论;
,证出EF=BE,即可得出结论;
(2)连接BE,由(1)可得出BE=BG=EF,证出![]() ,再由等腰直角三角形的性质即可得出结论;
,再由等腰直角三角形的性质即可得出结论;
(3)连接BE,证出CH=CF,证明![]() ,得出
,得出![]() ,证出
,证出![]() ,证明四边形
,证明四边形![]() 为正方形,得出∠FGB=90°,因此
为正方形,得出∠FGB=90°,因此![]() ,证明四边形
,证明四边形![]() 是平行四边形即可得出它是矩形.
是平行四边形即可得出它是矩形.
(1)证明:如图1所示:连接![]()
![]() ,
,
![]()
在![]() 和
和![]() 中,
中,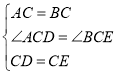
![]()
![]() ,
,![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
(2)解:![]()
理由如下:如图2所示,连接![]() .
.
由(1)可知,![]() ,
,
![]()
![]()
![]()
![]()
![]()
(3)证明:如图3所示,连接![]()
![]() ,
,
![]() ,
,![]()
![]() ,
,
![]()
![]() 与
与![]() 对称,点
对称,点![]() 的对应点为
的对应点为![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,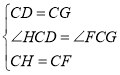
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
由(1)、(2)可知,![]() ,
,
![]() 四边形
四边形![]() 为正方形,
为正方形,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() 四边形
四边形![]() 为矩形
为矩形


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,图中每个小方格都是边长为1个单位长度的正方形,△ABC在方格纸中的位置如图所示.
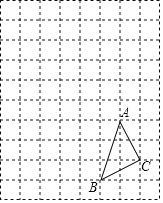
(1)请在图中建立平面直角坐标系,使得A,B两点的坐标分别为A(2,﹣1),B(1,﹣4),并写出C点坐标;
(2)在图中作出△ABC绕坐标原点旋转180°后的△A1B1C1,并写出A1,B1,C1的坐标;
(3)在图中作出△ABC绕坐标原点顺时针旋转90°后的△A2B2C2,并写出A2,B2,C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB=AD,对角线BD为⊙O的直径,AC与BD交于点E.点F为CD延长线上,且DF=BC.

(1)证明:AC=AF;
(2)若AD=2,AF=![]() ,求AE的长;
,求AE的长;
(3)若EG∥CF交AF于点G,连接DG.证明:DG为⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
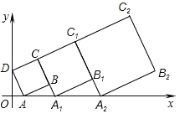
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第2012个正方形的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小明从中随机抽取一张卡片是足球社团B的概率是 .
(2)小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
如图,已知在△ABC 中,AB=AC,∠BAC=90°,点 A 在 x 轴上,点 B 在 y 轴上,点![]() 在二次函数
在二次函数![]() 的图像上.
的图像上.
(1)求二次函数的表达式;
(2)求点 A,B 的坐标;
(3)把△ABC 沿 x 轴正方向平移, 当点 B 落在抛物线上时, 求△ABC 扫过区域的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm.点E,F,G分别从A,B,C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为1.5cm/s.当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB'F,设点E,F,G运动的时间为t(单位:s).
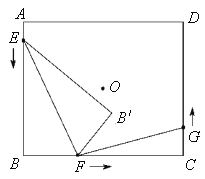
(1)当t= s时,四边形EBFB'为正方形;
(2)若以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形相似,求t的值;
(3)是否存在实数t,使得点B'与点O重合?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com