练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在下列解答中，填空或填写适当的理由：

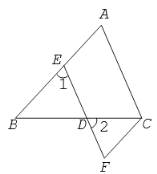
    （1），（已知）

    ______________.（___________________________________________）

    ________________（______________________________________）

    （2）_______，（已知）

    ；（___________________________________）

    （3）_______________，（已知）

    __________________________.（_______________________________）

    【答案】（1）见解析；（2）见解析；（3）见解析.

    【解析】

    （1）根据平行线的性质解答即可；

    （2）根据平行线的性质解答即可；

    （3）根据平行线的性质解答即可.

    （1）∵ AB∥CF，（已知）

    ∴ ∠1=∠ F ，（ 两直线平行，内错角相等 ）

    ∠A+∠ ACF =180°. （ 两直线平行，同旁内角互补）

    故答案为：F；两直线平行，内错角相等；ACF ；两直线平行，同旁内角互补

    （2）∵ ∠A=∠ 1 ，（ 已知 ）

    ∴ AC∥EF；（ 同位角相等，两直线平行 ）

    故答案为：1；同位角相等，两直线平行

    （3）∵ ∠2=∠ ACB ，（ 已知 ）

    ∴ AC ∥ EF ；（ 内错角相等，两直线平行 ）

    故答案为：ACB；AC；EF；内错角相等，两直线平行

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，在中，AB=AC，∠ABC =，D是BC边上一点，以AD为边作，使AE=AD，+=180°．

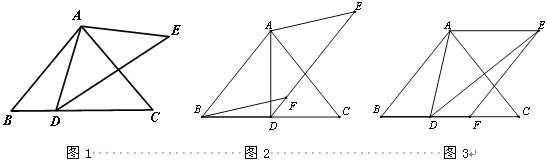
    （1）直接写出∠ADE的度数（用含的式子表示）；

    （2）以AB，AE为边作平行四边形ABFE，

    ①如图2，若点F恰好落在DE上，求证：BD=CD；

    ②如图3，若点F恰好落在BC上，求证：BD=CF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，△ABC中，AC=BC，∠A=30°，点D在AB边上且∠ADC=45°．

    （1）求∠BCD的度数；

    （2）将图①中的△BCD绕点B顺时针旋转，得到△BC′D′．当点D′恰好落在BC边上时，如图②所示，连接C′C并延长交AB于点E．

    ①求∠C′CB的度数；

    ②求证：△C′BD′≌△CAE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

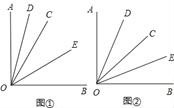
    【题目】已知∠AOB是一个直角，作射线OC，再分别作∠AOC和∠BOC的平分线OD，OE．

    （1）如图①，当∠BOC＝40°时，求∠DOE的度数；

    （2）如图②，当射线OC在∠AOB内绕O点旋转时，∠DOE的大小是否发生变化，说明理由；

    （3）当射线OC在∠AOB外绕O点旋转且∠AOC为钝角时，画出图形，直接写出∠DOE的度数（不必写过程）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】.分别是数轴上两个不同点A.B所表示的有理数，且，，A.B两点在数轴上的位置如图所示：

    （1）数＝_____；＝______；

    （2）A.B两点相距多少个单位长度？

    （3）点P从A点出发，先向左移动一个单位长度，再向右移动2个单位长度，再向左移动3个单位长度，再向右移动4个单位长度，依次操作2020次后，求P点表示的数.

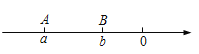
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某路公交车从起点站出发依次经过A、B、C站到达终点站，各站上、下乘客人数如下表所示(记上车人数为正，下车人数为负)．

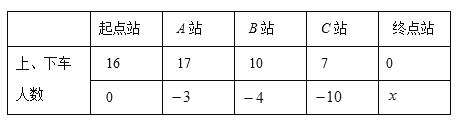
    (1)表格中的值是 ；

    (2)若此公交车采用一票制，即每位上车乘客无论哪站下车，车票都是2元，问该车这次出车共收入多少元？请列式计算．

    (3)通过列式计算，公交车行驶在哪两站之间时车上的乘客最多？最多乘客人数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】点在数轴上分别表示有理数，两点间的距离表示为．且．

    （1）数轴上表示2和5的两点之间的距离是___，

    数轴上表示2和5的两点之间的距离是___，

    数轴上表示1和3的两点之间的距离是___；

    (2)数轴上表示x和1的两点A和B之间的距离是___，如果|AB|=2，那么x=___；

    (3)当代数式|x+1|+|x2|取最小值时，相应x的取值范围是___.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在△ABC中，AB=AC，以AC为直径的⊙O与BC交于点D，DE⊥AB，垂足为E，ED的延长线与AC的延长线交于点F。

    （1）求证：DE是⊙O的切线；

    （2）若⊙O的半径为4，BE=2，求∠F的度数。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 （用如图所示的曲尺形框框（有三个方向），可以套住下表中的三个数，设被框住的三个数中（第一个框框住的最小的数为a、第二个框框住的最小的数为b、第三个框框住的最小的数为c）.

    （1）第一个框框住的三个数中最小的数为a,三个数的和是: ；第二个框框住的三个数中最小的数为b,三个数的和是: ；第三个框框住的三个数中最小的数为c,三个数的和是: ；

    （2）这三个框框住的数的和能是48吗？，能，求出最小的数a、b、c的值.

    查看答案和解析>>

    同步练习册答案