
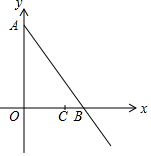
 如图:在平面直角坐标系中,点O为坐标原点,△AOB的面积为18$\sqrt{3}$,∠ABO=60°,点C在OB上,OC=4,BC=2,动点P从A点出发沿射线AB以每秒2个单位的速度运动,连接OP.
如图:在平面直角坐标系中,点O为坐标原点,△AOB的面积为18$\sqrt{3}$,∠ABO=60°,点C在OB上,OC=4,BC=2,动点P从A点出发沿射线AB以每秒2个单位的速度运动,连接OP.分析 (1)在Rt△AOB中,因为∠ABO=60°,∠AOB=90°,所以∠AOB=30°,设OB=a,则AB=2a,OA=$\sqrt{3}$a,利用三角形面积公式即可求出a,解决问题.
(2)分两种情形①当0≤t<6时,②当t>6时分别求解即可.
(3)如图2中,作PN⊥x轴于N.只要证明△QPH≌△PCN,推出PH=CN=6,由BC=2,推出BN=4,因为∠BON=30°,∠PNB=90°,推出PB=2BN=8,推出AP=AB+PB=12+8=20,即可解决问题.
解答 解:(1)在Rt△AOB中,
∵∠ABO=60°,∠AOB=90°,
∴∠AOB=30°,设OB=a,则AB=2a,OA=$\sqrt{3}$a,
∵$\frac{1}{2}$•OB•OA=18$\sqrt{3}$,
∴$\frac{1}{2}$•a•$\sqrt{3}$a=18$\sqrt{3}$,
∴a=6,
∴OA=6$\sqrt{3}$,
∴点A坐标(0,6$\sqrt{3}$).
(2)如图1中,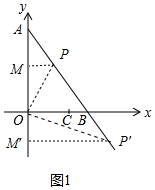
①当0≤t<6时,作PM⊥OA于M,
∵PA=2t,∠PAM=30°,
∴PM=$\frac{1}{2}$PA=t,
∴S△POB=S△AOB-S△AOP=18$\sqrt{3}$-$\frac{1}{2}$$•6\sqrt{3}$•t=-3$\sqrt{3}$t+18$\sqrt{3}$,
②当t>6时,作P′M′⊥OA于M′,
∵P′A=2t,∠P′AM′=30°,
∴P′M′=$\frac{1}{2}$P′A=t,
∴S△P′OB=S△P′AO-S△AOB=$\frac{1}{2}$$•6\sqrt{3}$•t-18$\sqrt{3}$=3$\sqrt{3}$t-18$\sqrt{3}$.
综上所述,S=$\left\{\begin{array}{l}{-3\sqrt{3}t+18\sqrt{3}}&{(0≤t<6)}\\{3\sqrt{3}t-18\sqrt{3}}&{(t>6)}\end{array}\right.$.
(3)如图2中,作PN⊥x轴于N.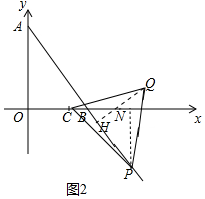
∵∠NBP=∠ABO=60°,
∴∠BCP+∠BPC=60°,∵∠BPC+∠QPH=60°,
∴∠QPH=∠PCN,
∵∠QHP=∠PNC=90°,PQ=PC,
∴△QPH≌△PCN,
∴PH=CN=6,
∵BC=2,
∴BN=4,
∵∠BON=30°,∠PNB=90°,
∴PB=2BN=8,
∴AP=AB+PB=12+8=20,
∴t=10,
点评 本题考查几何变换综合题、直角三角形30度角性质、三角形的面积、全等三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
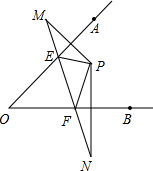 如图,点P在∠AOB的内部,点M,N分别是点P关于直线OA,OB的对称点,线段MN交OA,OB于点E,F.
如图,点P在∠AOB的内部,点M,N分别是点P关于直线OA,OB的对称点,线段MN交OA,OB于点E,F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
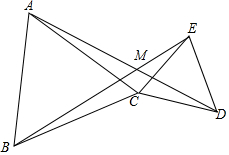 如图,两个等腰角形△CAB与△CED,其CA=CB,CE=CD,∠ACB=∠ECD=α,连接AD、CE.求证:
如图,两个等腰角形△CAB与△CED,其CA=CB,CE=CD,∠ACB=∠ECD=α,连接AD、CE.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
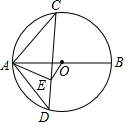 如图,AB是⊙O的直径,C是半圆的中点,连接CA,E是弦CD上一点,CE=CA,连接AD.
如图,AB是⊙O的直径,C是半圆的中点,连接CA,E是弦CD上一点,CE=CA,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
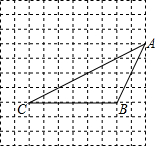 如图是由100个边长为1的小正方形组成的10×10的正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形.
如图是由100个边长为1的小正方形组成的10×10的正方形网格,设顶点在这些小正方形顶点的三角形为格点三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com