
【题目】如图,直线m,n交于点B,m、n的夹角为50°,点A是直线m上的点,在直线n上寻找一点C,使△ABC是等腰三角形,这样的C点有多少个?( ) 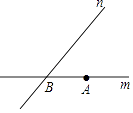
A.1个
B.2个
C.3个
D.4个
科目:初中数学 来源: 题型:
【题目】一粒芝麻约有0.000002千克,0.000002用科学记数学法表示为( )千克.
A.2×10﹣4
B.0.2×10﹣5
C.2×10﹣7
D.2×10﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
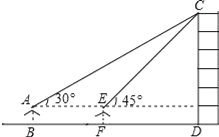
【题目】某数学兴趣小组在学习了《锐角三角函数》以后,开展测量物体高度的实践活动,测量一建筑物CD的高度,他们站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走20m,到达点F处测得楼顶C的仰角为45°(BFD在同一直线上).已知观测员的眼睛与地面距离为1.5m(即AB=1.5m),求这栋建筑物CD的高度.(参考数据: ![]() ≈1.732,
≈1.732, ![]() ≈1.414.结果保留整数)
≈1.414.结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
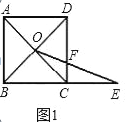
【题目】数学课上,张老师出示了问题1:如图1,四边形ABCD是正方形,BC=1,对角线交点记作O,点E是边BC延长线上一点.连接OE交CD边于F,设CE=x,CF=y,求y关于x的函数解析式及其定义域.
(1)经过思考,小明认为可以通过添加辅助线﹣﹣过点O作OM⊥BC,垂足为M求解.你认为这个想法可行吗?请写出问题1的答案及相应的推导过程;
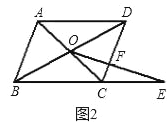
(2)如果将问题1中的条件“四边形ABCD是正方形,BC=1”改为“四边形ABCD是平行四边形,BC=3,CD=2,”其余条件不变(如图2),请直接写出条件改变后的函数解析式;
(3)如果将问题1中的条件“四边形ABCD是正方形,BC=1”进一步改为:“四边形ABCD是梯形,AD∥BC,BC=a,CD=b,AD=c(其中a,b,c为常量)”其余条件不变(如图3),请你写出条件再次改变后y关于x的函数解析式以及相应的推导过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道不等式的两边加(或减)同一个数(或式子)不等号的方向不变.不等式组是否也具有类似的性质?请完成下列填空(填“>”或“<”),探索归纳得到一般的关系式:
(1)已知![]() 可得5+2 3+1,已知
可得5+2 3+1,已知![]() 可得﹣5﹣2 ﹣3﹣1;
可得﹣5﹣2 ﹣3﹣1;
已知![]() 可得﹣2+1 3+4,…,一般地,如果
可得﹣2+1 3+4,…,一般地,如果![]() , 那么a+c b+d.
, 那么a+c b+d.
(2)应用不等式的性质证明上述关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,第一象限内长方形ABCD,AB∥y轴,点A(1,1),点C(a,b),满足![]() +|b﹣3|=0.
+|b﹣3|=0.
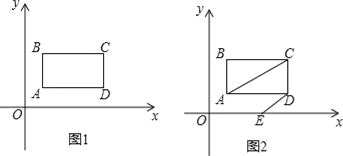
(1)求长方形ABCD的面积.
(2)如图2,长方形ABCD以每秒1个单位长度的速度向右平移,同时点E从原点O出发沿x轴以每秒2个单位长度的速度向右运动,设运动时间为t秒.
①当t=4时,直接写出三角形OAC的面积为 ;
②若AC∥ED,求t的值;
(3)在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点,已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An.
①若点A1的坐标为(3,1),则点A3的坐标为 ,点A2014的坐标为 ;
②若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,∠BAD=90°,以点B为圆心,BC长为半径画弧,与射线AD相交于点E,连接BE,过C点作CF⊥BE,垂足为F.线段BF与图中现有的哪一条线段相等?先将你猜想出的结论填写在下面的横线上,然后再加以证明.
结论:BF= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司准备投资开发A、B两种新产品,信息部通过调研得到两条信息:
信息一:如果投资A种产品,所获利润![]() (万元)与投资金额x(万元)之间满足正比例函数关系:
(万元)与投资金额x(万元)之间满足正比例函数关系: ![]() ;
;
信息二:如果投资B种产品,所获利润![]() (万元)与投资金额x(万元)之间满足二次函数关系:
(万元)与投资金额x(万元)之间满足二次函数关系: ![]() ;
;
根据公司信息部报告, ![]() 、
、![]() (万元)与投资金额x(万元)的部分对应值如下表所示:
(万元)与投资金额x(万元)的部分对应值如下表所示:
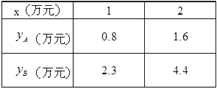
(1)填空: ![]() = ;
= ; ![]() = ;
= ;
(2)如果公司准备投资20万元同时开发A、B两种新产品,设公司所获得的总利润为W(万元),B种产品的投资金额为x(万元),则A种产品的投资金额为_________万元,并求出W与x之间的函数关系式;
(3)请你设计一个在(2)中公司能获得最大总利润的投资方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据统计2015年宁波市实现地区生产总值8011.5亿元,按可比价格计算,比上年增长了8%,把8011.5亿用科学记数法表示是( )
A.8011.5×108
B.801.15×109
C.8.0115×1010
D.8.0115×1011
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com