
【题目】如图,正方形ABCD中,AB=3,点E是对角线AC上的一点,连接DE,过点E作EF⊥DE,交AB于点F,连接DF交AC于点G,下列结论:
①DE=EF;②∠ADF=∠AEF;③DG2=GEGC;④若AF=1,则EG=![]() ,其中结论正确的个数是( )
,其中结论正确的个数是( )
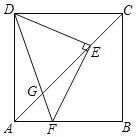
A. 1B. 2C. 3D. 4
【答案】D
【解析】
证明△DCE≌△BCE,得DE=BE,证出EF=BE,则结论①正确;易证∠EDF=∠DFE=45°,又∠DAC=45°,∠AGD=∠EGF,则∠ADF=∠AEF,故②正确;证出△DGE∽△CGD,由比例线段可得出结论DG2=GEGC,③正确;先求出CE长,将△DEC绕点A逆时针旋转90°得到△DMA,连接MG,易证△DMG≌△DEG,△AMG是直角三角形,得出EG2=AG2+CE2,设EG=x,则列出方程可求出EG=![]() ,则④正确.
,则④正确.
解:如图,连接BE,
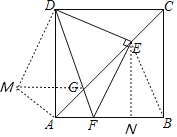
∵四边形ABCD为正方形,
∴CB=CD,∠BCE=∠DCE=45°,
在△BEC和△DEC中,
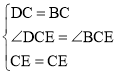 ,
,
∴△DCE≌△BCE(SAS),
∴DE=BE,∠CDE=∠CBE,
∴∠ADE=∠ABE,
∵∠DAB=90°,∠DEF=90°,
∴∠ADE+∠AFE=180°,
∵∠AFE+∠EFB=180°,
∴∠ADE=∠EFB,
∴∠ABE=∠EFB,
∴EF=BE,
∴DE=EF,故①正确;
∵∠DEF=90°,DE=EF,
∴∠EDF=∠DFE=45°,
∵∠DAC=45°,∠AGD=∠EGF,
∴∠ADF=∠AEF,故②正确;
∵∠GDE=∠DCG=45°,∠DGE=∠CGD,
∴△DGE∽△CGD,
∴![]() ,
,
即DG2=GECG,故③正确;
如图,过点E作EN⊥AB于点N,
∵AF=1,AB=3,
∴BF=2,AC=![]() ,
,
∵BE=EF,
∴FN=BN=1,
∴AN=2,
∴![]() ,
,
∴![]() ,
,
将△DEC绕点A逆时针旋转90°得到△DMA,连接MG,
易证△DMG≌△DEG(SAS),△AMG是直角三角形,
∴MG=GE,
∴MG2=EG2=AM2+AG2=CE2+AG2,
设EG=x,则AG=![]() ,
,
∴![]() ,
,
解得:x=![]() ,即EG=
,即EG=![]() ,故④正确.
,故④正确.
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别交x轴、y轴于点B,C,正方形AOCD的顶点D在第二象限内,E是BC中点,OF⊥DE于点F,连结OE,动点P在AO上从点A向终点O匀速运动,同时,动点Q在直线BC上从某点Q1向终点Q2匀速运动,它们同时到达终点.
分别交x轴、y轴于点B,C,正方形AOCD的顶点D在第二象限内,E是BC中点,OF⊥DE于点F,连结OE,动点P在AO上从点A向终点O匀速运动,同时,动点Q在直线BC上从某点Q1向终点Q2匀速运动,它们同时到达终点.
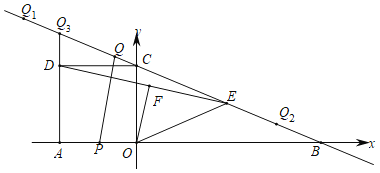
(1)求点B的坐标和OE的长;
(2)设点Q2为(m,n),当![]() tan∠EOF时,求点Q2的坐标;
tan∠EOF时,求点Q2的坐标;
(3)根据(2)的条件,当点P运动到AO中点时,点Q恰好与点C重合.
①延长AD交直线BC于点Q3,当点Q在线段Q2Q3上时,设Q3Q=s,AP=t,求s关于t的函数表达式.
②当PQ与△OEF的一边平行时,求所有满足条件的AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
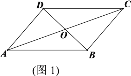
【题目】我们把有两边对应相等,且夹角互补(不相等)的两个三角形叫做“互补三角形”,如图1,□ABCD中,△AOB和△BOC是“互补三角形”.
(1)写出图1中另外一组“互补三角形”_______;
(2)在图2中,用尺规作出一个△EFH,使得△EFH和△EFG为“互补三角形”,且△EFH和△EFG在EF同侧,并证明这一组“互补三角形”的面积相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=12cm,AD=CD=8cm,动点E从点A出发沿AB以每秒1cm的速度向点B运动,动点F从点B出发沿BA以每秒1cm的速度向点A运动,过点E作AB的垂线交折线AD-DC于点G,以EG、EF为邻边作矩形EFHG,设点E、F运动的时间为t(秒),矩形EFHG与四边形ABCD重叠部分的面积为S(cm2).
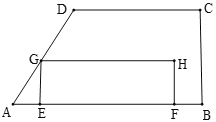
(1)求EG的长(用含t的代数式表示);
(2)当t为何值时,点G与点D重合?
(3)当点G在DC上时,求S(cm2)与t(秒)的函数关系式(S>0);
(4)连接EH、GF、AC、BD,在运动过程中,当这四条线段所在的直线有两条平行时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:

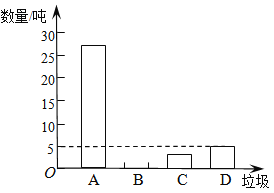
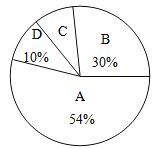
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在抽样数据中,产生的有害垃圾共 吨;
(3)调查发现,在可回收物中塑料类垃圾占![]() ,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更精准地关爱留守学生,某学校将留守学生的各种情形分成四种类型:A.由父母一方照看;B.由爷爷奶奶照看;C.由叔姨等近亲照看;D.直接寄宿学校.某数学小组随机调查了一个班级,发现该班留守学生数量占全班总人数的20%,并将调查结果制成如下两幅不完整的统计图.
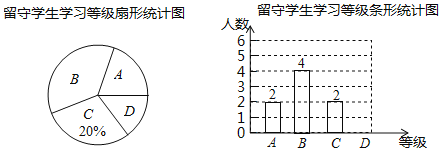
(1)该班共有 名留守学生,B类型留守学生所在扇形的圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)已知该校共有2400名学生,现学校打算对D类型的留守学生进行手拉手关爱活动,请你估计该校将有多少名留守学生在此关爱活动中受益?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
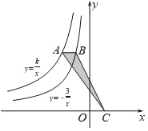
【题目】如图,点A是反比例函数y=![]() 图象上一点,过点A作x轴的平行线交反比例函数y=﹣
图象上一点,过点A作x轴的平行线交反比例函数y=﹣![]() 的图象于点B,点C在x轴上,且S△ABC=
的图象于点B,点C在x轴上,且S△ABC=![]() ,则k=( )
,则k=( )
A. 6B. ﹣6C. ![]() D. ﹣
D. ﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法,学校采取随机抽样的方法进行问卷调查![]() 每个被调查的学生必须选择而且只能选择其中一门
每个被调查的学生必须选择而且只能选择其中一门![]() 对调查结果进行整理,绘制成如下两幅不完整的统计图
对调查结果进行整理,绘制成如下两幅不完整的统计图![]() 请结合图中所给信息解答下列问题:
请结合图中所给信息解答下列问题:


![]() 本次调查的学生共有______人,在扇形统计图中,m的值是______.
本次调查的学生共有______人,在扇形统计图中,m的值是______.
![]() 分别求出参加调查的学生中选择绘画和书法的人数,并将条形统计图补充完整.
分别求出参加调查的学生中选择绘画和书法的人数,并将条形统计图补充完整.
![]() 该校共有学生2000人,估计该校约有多少人选修乐器课程?
该校共有学生2000人,估计该校约有多少人选修乐器课程?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com