练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．先化简，再求值：$\frac{x}{x-1}$+$\frac{x+1}{{x}^{2}-1}$，其中x=2．

    分析 原式通分并利用同分母分式的减法法则计算得到最简结果，把x的值代入计算即可求出值．

    解答 解：原式=$\frac{x}{x-1}$+$\frac{1}{x-1}$=$\frac{x+1}{x-1}$，
    当x=2时，原式=3．

    点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    4．请写出一个无理数$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．在平行四边形ABCD中，对角线AC与BD相交于点O，要使四边形ABCD是正方形，还需添加一组条件．下面给出了四组条件：①AB⊥AD，且AB=AD；②AB=BD，且AB⊥BD；③OB=OC，且OB⊥OC；④AB=AD，且AC=BD．其中正确的序号是①③④．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

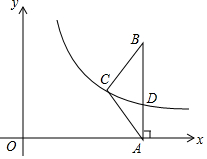    2．如图，在△ABC中，AC=BC，AB⊥x轴，垂足为A．反比例函数y=$\frac{k}{x}$（x＞0）的图象经过点C，交AB于点D．已知AB=4，BC=$\frac{5}{2}$．
    （1）若OA=4，求k的值；
    （2）连接OC，若BD=BC，求OC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图，在△ABC中，∠ACB=90°，点D，E，F分别是AB，BC，CA的中点，若CD=2，则线段EF的长是2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，在平面直角坐标系xOy中，抛物线y=x2-2x-3交x轴于A，B两点（点A在点B的左侧），将该抛物线位于x轴上方曲线记作M，将该抛物线位于x轴下方部分沿x轴翻折，翻折后所得曲线记作N，曲线N交y轴于点C，连接AC、BC．
    （1）求曲线N所在抛物线相应的函数表达式；
    （2）求△ABC外接圆的半径；
    （3）点P为曲线M或曲线N上的一动点，点Q为x轴上的一个动点，若以点B，C，P，Q为顶点的四边形是平行四边形，求点Q的坐标．

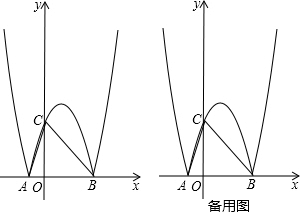
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．“购买某种苹果所花的钱y（元）与购买苹果的重量x（kg）之间的函数关系如图，且每进店购买一次，必须同时购买一个0.4元的塑料袋”，这是某水果店的广告，小娟上午买了苹果1kg，下午又买了2kg，若将她两次花的钱一次性购买此苹果（含塑料袋），则可多买苹果（　　）
    A．$\frac{2}{5}$kgB．$\frac{2}{3}$kgC．$\frac{4}{5}$kgD．$\frac{14}{15}$kg

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．要使（x2-2x+b）（x-a）中不含x的一次项和二次项，则a，b的值分别为（　　）
    A．a=-2，b=-4B．a=2，b=4C．a=2，b=-4D．a=-2，b=4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．如图：∠ABC=∠DEF，∠A=∠D，要证明△ABC≌△DEF，需要添加一个条件为AB=DE（只添加一个条件即可）．

    查看答案和解析>>

    同步练习册答案