
【题目】如图,两个以点O为圆心的同心圆,
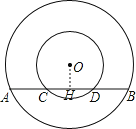
(1)如图1,大圆的弦AB交小圆于C,D两点,试判断AC与BD的数量关系,并说明理由.
(2)如图2,将大圆的弦AB向下平移使其为小圆的切线,切点为C,证明:AC=BC.
(3)在(2)的基础上,已知AB=20cm,直接写出圆环的面积.

图1 图2
【答案】(1)AC=BD;(2)见解析;(3)100πcm2
【解析】试题分析:作OH⊥AB于H,根据垂径定理得到AH=BH,CH=DH,然后利用等量减等量差相等可得到结论.
(2) 根据切线的性质以及垂径定理即可证明;
(3)根据圆环的面积等于两圆的面积差,再根据切线的性质定理、勾股定理、垂径定理求解.
试题解析:(1)AC=BD,理由是:
过O作OH⊥AB,由垂径定理得AH=BH,CH=DH,
AH-CH=BH-DH,
即AC=BD
(2)连接OC,如图,
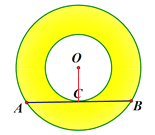
AB是小圆的切线,
OC⊥AB,则AC=BC
(3)如图,连接OB.
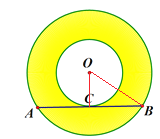
∵大圆的弦AB是小圆的切线,
∴OC⊥AB,AC=CB,
∴OB2-OC2=(20÷2)2=102,
∵S圆环=S大-S小=πOB2-πOC2=π(OB2-OC2),
∴S圆环=100πcm2


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为一个矩形纸片,AB=3,BC=2,动点P自D点出发沿DC方向运动至C点后停止,△ADP以直线AP为轴翻折,点D落在点D1的位置,设DP=x,△AD1P与原纸片重叠部分的面积为y.

(1)当x为何值时,直线AD1过点C?
(2)当x为何值时,直线AD1过BC的中点E?
(3)求出y与x的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个长方形操场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.
(1)请列式表示操场空地的面积;
(2)若休闲广场的长为 50米,宽为20米,圆形花坛的半径为 3米,求操场空地的面积.(π取 3.14,计算结果保留 0.1)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax![]() +bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①抛物线与x轴的另一个交点是(5,0);②4a+c>2b;③4a+b=0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( )
+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①抛物线与x轴的另一个交点是(5,0);②4a+c>2b;③4a+b=0;④当x>-1时,y的值随x值的增大而增大.其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新建小区要在一块等边三角形内修建一个圆形花坛.
(1)要使花坛面积最大,请你用尺规画出圆形花坛示意图;(保留作图痕迹,不写做法)
(2)若这个等边三角形的周长为36米,请计算出花坛的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)y(x+y)+(x+y)(x-y)-x2,其中x=-2,y=![]() ;
;
(2)(x+y)2-2x(x+y),其中x=3,y=2.
(3)(a+b)2-2a(b+1)-a2b÷b,其中a=-2,b=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点P关于OA、OB的对称点分别是P1,P2,线段P1P2分别交OA、OB于D、C,P1P2=6cm,则△PCD的周长为( )

A.3cmB.6cmC.12cmD.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.

(1)求证:四边形ABCD是菱形;
(2)若∠ADB=30°,BD=12,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com