
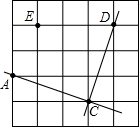
 如图,在下面的格点图中,直线AC与CD相交于点C.
如图,在下面的格点图中,直线AC与CD相交于点C.科目:初中数学 来源: 题型:



查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省太仓市七年级下学期期中考试数学试卷(带解析) 题型:解答题
教材第66页探索平方差公式时设置了如下情境:边长为b的小正方形纸片放置在边长为a的
大正方形纸片上(如图9?6),你能通过计算未盖住部分的面积得到公式(a + b) (a ? b) = a2? b2吗?
(不必证明)
(1)如果将小正方形的一边延长(如图①),是否也能推导公式?请完成证明.
(2) 面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”.例如,著名的赵爽弦图(如图②,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2,也可以表示为4´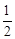 ab + (a ? b)2,由此推导出重要的勾股定理:a2 + b2 = c2.
ab + (a ? b)2,由此推导出重要的勾股定理:a2 + b2 = c2.
图③为美国第二十任总统伽菲尔德的“总统证法”,请你完成证明.

(3) 试构造一个图形,使它的面积能够解释(a ? 2b)2 = a2? 4ab + 4b2,画在下面的格点中,并标出字母a、b所表示的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
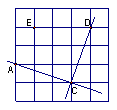
如图,在下面的格点图中,直线AC与CD相交于点C。
(1)过点E画直线EF,使EF⊥AC;
(2)分别表示⑴中三条直线之间的位置关系。
(3)由此你能得到什么结论?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com