
【题目】方格纸中小正方形的顶点叫格点.点A和点B是格点,位置如图.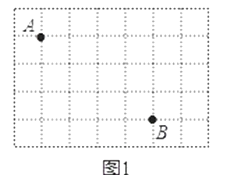
(1)在图1中确定格点C使△ABC为直角三角形,画出一个这样的△ABC;
(2)在图2中确定格点D使△ABD为等腰三角形,画出一个这样的△ABD;
(3)在图2中满足题(2)条件的格点D有个.
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(8,8),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.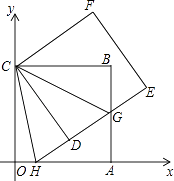
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;判断线段HG、OH、BG的数量关系,并说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中, AB、BC、AC三边的长分别为 ![]() 、
、 ![]() 、
、 ![]() ,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.
,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.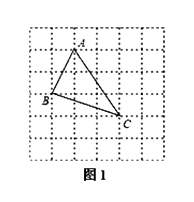
(1)△ABC的面积为: .
(2)若△DEF三边的长分别为 ![]() 、
、 ![]() 、
、 ![]() ,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积.
,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积.
(3)如图3,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13、10、17,请利用第2小题解题方法求六边形花坛ABCDEF的面积.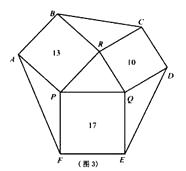
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰三角形一腰上的高线等于腰长的一半,那么这个等腰三角形的一个底角等于( )
A. 15°或75° B. 15° C. 75° D. 150°和30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(4,0),点B的坐标为(0,b)(b>0),点P是直线AB上位于第二象限内的一个动点,过点P作PC⊥x轴于点C,记点P关于y轴的对称点为Q,设点P的横坐标为a.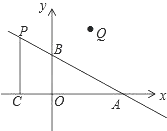
(1)当b=3时,
①求直线AB的解析式;
②若QO=QA,求P点的坐标.
(2)是否同时存在a、b,使得△QAC是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列长度的三根小木棒,能构成三角形的是
A. 2cm,5cm,7cm B. 6cm,10cm,17cm
C. 5cm,5cm,12cm D. 12cm,15cm,20cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com