
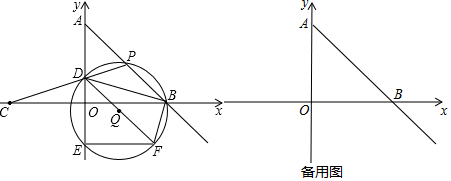
���� ��1���ֱ���x��y����0��ö�Ӧ��y��x��ֵ�������A�͵�B�����꣬Ȼ��������ԳƵ����ʿ���õ�C�����ꣻ
��2������P��AB��ʱ������EP�����ȿ�֤����AOBΪ����ֱ�������Σ�Ȼ����֤����ADP=��BPE��Ȼ�����������ε���ǵ����ʿ�֤����DPE=��DAP=45�㣬����Բ�ܽǶ�������á�DFE=45�㣬��DEF=90�㣻����P��AB���ӳ�����ʱ������BE��ͬ����֤����DFE=45�㣮����DEF=90�㣻
��3����֤����DOQΪ����ֱ�������Σ�����DQ=a����QB=$\sqrt{2}$a��Ȼ�����OQ+BQ=4�������a��ֵ��Ȼ������CD�Ľ���ʽ�������������ֱ��AB��ֱ��CD�Ľ������꼴�ɣ�
��� �⣺��1����x=0�ã�y=4��
���A��������0��4����
��y=0�ã�-x+4=0����ã�x=4��
���B��������4��0����
�ߵ�C���B����y��Գƣ�
���C��-4��0����
��2����ͼ1��ʾ������EP��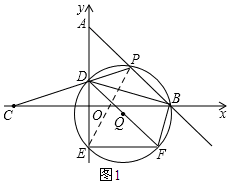
�ߵ�B������Ϊ��4��0������A������Ϊ��0��4����
��OA=OB��
���OAB=45�㣮
�ߵ�B���C����y��Գƣ�
���CDO=��BDO��
�֡ߡ�CDO=��ADP��
���BDE=��ADP��
�֡ߡ�BDE=��BPE��
���ADP=��BPE��
�ߡ�DAP+��ADP=��DPE+��BPE=��DPB��
���DPE=��DAP=45�㣮
���DFE=45�㣮
��DFΪ��Q��ֱ����
���DEF=90�㣬
���DEFΪ����ֱ�������Σ�
��ͼ2��ʾ������BE��
�ߵ�B���C����y��Գƣ�
���ADB=��ADC��
�֡ߡ�ADC=��EDP����DEP=��EBP��
���ADB=��EBP��
�ߡ�ADB+��DAB=��BEP+��DBE��
���DBE=��DAB=45�㣮
���DFE=45�㣮
��DFΪ��Q��ֱ����
���DEF=90�㣮
���DEFΪ����ֱ�������Σ�
��3����ͼ3��ʾ��
�ɣ�2����֪��DEFΪ����ֱ�������Σ����EDF=45�㣮
�ߡ�DOB=90�㣬��DOQ=45�㣬
���DOQΪ����ֱ�������Σ�
��OD=OQ��
��DO=OQ=a����QD=$\sqrt{2}$a����QB=QD=$\sqrt{2}$a��
��OQ+BQ=4��
��a+$\sqrt{2}a$=4����ã�a=4$\sqrt{2}$-4��
��CD�Ľ���ʽΪy=kx+4$\sqrt{2}$-4������C���������ã�-4k+4$\sqrt{2}$-4=0�����k=$\sqrt{2}$-1��
��ֱ��CD�Ľ���ʽΪy=��$\sqrt{2}$-1��x+4$\sqrt{2}$-4��
��y=-x+4��y=��$\sqrt{2}$-1��x+4$\sqrt{2}$-4���������x=4$\sqrt{2}$-4��y=8-4$\sqrt{2}$��
���P��������4$\sqrt{2}$-4��8-4$\sqrt{2}$����
���� ������Ҫ�������Բ���ۺ�Ӧ�ã��������ҪӦ����Բ�ܽǶ���������������Գ�ͼ�ε����ʣ�����ֱ�������ε����ʺ��ж�������ϵ������һ�κ����Ľ���ʽ�Լ���ֱ�ߵĽ��������֪ʶ�㣬��á�DBE���DPE�Ķ����ǽ���Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����֪AB=CD��AD=BC���������н��ۣ�
��ͼ����֪AB=CD��AD=BC���������н��ۣ�| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��a��c�ļн��ǡϦ���ֱ��b��c�ļн��ǡϦ£���ֱ��a���ơ���A����ʱ�뷽����ת�����Ϧ���Ϧ�����Ϧ�+�Ϧ�=180��ʱ��ֱ��a��b��������ͬ���ڽǻ�������ֱ��ƽ�У�
��ͼ��ֱ��a��c�ļн��ǡϦ���ֱ��b��c�ļн��ǡϦ£���ֱ��a���ơ���A����ʱ�뷽����ת�����Ϧ���Ϧ�����Ϧ�+�Ϧ�=180��ʱ��ֱ��a��b��������ͬ���ڽǻ�������ֱ��ƽ�У��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6$\sqrt{2}$ | B�� | 2$\sqrt{12}$ | C�� | 6 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ó�32�����Χ�����Ϊ130m2�ľ��γ��أ����γ��ص�һ������ǽ�������Ϊ16m����ǽƽ�еĶԱ���1m����һ���ţ���˾��γ��صij��������Ƕ����ף�
�ó�32�����Χ�����Ϊ130m2�ľ��γ��أ����γ��ص�һ������ǽ�������Ϊ16m����ǽƽ�еĶԱ���1m����һ���ţ���˾��γ��صij��������Ƕ����ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com