
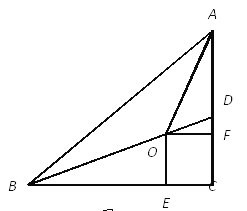
【题目】如图,在Rt△ABC中,∠C=90,BD是△ABC的角平分线,点O在BD上,分别过点O作OE⊥BC,OF⊥AC,垂足为E,F,且OE=OF.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
【答案】(1)证明见解析;(2)OE=2.
【解析】试题分析:(1)过点O作OM⊥AB,由角平分线的性质得OE=OM,由正方形的性质得OE=OF,易得OM=OF,由角平分线的判定定理得点O在∠BAC的平分线上;
(2)连接OC,根利用勾股定理求出AB的长,据三角形的面积公式即可得出结论.
试题解析:(1)证明:过点O作OM⊥AB于点M.
因为BD平分∠ABC,OM⊥AB于M,OE⊥BC于E,所以OM=OE.
又OE=OF,所以OM=OF.所以点O在∠BAC的平分线上.
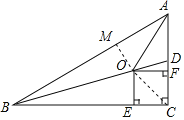
(2)连接OC.在Rt△ABC中,∠C=90°,AC=5,BC=12,根据勾股定理,得AB=13.
因为S△ABO+S△BCO+S△ACO =S△ABC,所以![]() ×13·OM+
×13·OM+![]() ×12·OE+
×12·OE+![]() ×5·OF=
×5·OF=![]() ×5×12.
×5×12.
由(1)知OM=OE=OF,所以15OE=30,解得OE=2.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.相等的角是对顶角
B.在同一平面内,不平行的两条直线一定互相垂直
C.点P(2,﹣3)在第四象限
D.一个数的算术平方根一定是正数
查看答案和解析>>
科目:初中数学 来源: 题型:
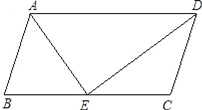
【题目】如图,已知平行四边形ABCD,DE是∠ADC的角平分线,交BC于点E.
(1)求证:CD=CE;
(2)若BE=CE,∠B=80°,求∠DAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)计算:3( ![]() ﹣π)0﹣
﹣π)0﹣ ![]() +(﹣1)2011
+(﹣1)2011
(2)先化简,再求值: ![]() ,其中x=
,其中x= ![]() -3.
-3.
(3)如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,且AF=CE,BH=DG. 求证:GF∥HE.
查看答案和解析>>
科目:初中数学 来源: 题型:
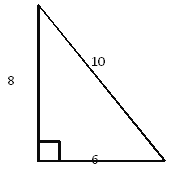
【题目】如图,已知一个边长分别为6、8、10的直角三角形,请设计出一个有一条边长为8的直角三角形,使这两个直角三角形能够拼成一个等腰三角形.
(1)画出4种不同拼法(周长不等)的等腰三角形;
(2)分别求出4种不同拼法的等腰三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用1─9中的三个数字,如2、3、5组成数字不重复的三位整数,共有6个,计算方法为:3×2×1=6,现有1个老师和4个学生站成一排照相,老师站在正中间的不同站法有______种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好地保护美丽如画的邛海湿地,西昌市污水处理厂决定先购买A,B两种型号的污水处理设备共20台,对邛海湿地周边污水进行处理.每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640 t,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1 080 t.
(1)求A,B两种型号的污水处理设备每周每台分别可以处理污水多少吨.
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4 500 t,请你列举出所有购买方案,并指出哪种方案所需资金最少,最少是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,我们曾经研究过n×n的正方形网格,得到了网格中正方形的总数的表达式为12+22+32+…+n2 . 但n为100时,应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题.首先,通过探究我们已经知道0×1+1×2+2×3+…+(n﹣l)×n
= ![]() n(n+1)(n﹣1)时,我们可以这样做:
n(n+1)(n﹣1)时,我们可以这样做:
(1)观察并猜想:
12+22=(1+0)×1+(1+1)×2=l+0×1+2+1×2=(1+2)+(0×1+1×2)
12+22+32=(1+0)×1+(1+1)×2+(l+2)×3
=1+0×1+2+1×2+3+2×3
=(1+2+3)+(0×1+1×2+2×3)
12+22+32+42=(1+0)×1+(1+1)×2+(l+2)×3+
=1+0×1+2+1×2+3+2×3+
=(1+2+3+4)+()
…
(2)归纳结论:
12+22+32+…+n2=(1+0)×1+(1+1)×2+(1+2)×3+…[1+(n﹣l)]n
=1+0×1+2+1×2+3+2×3+…+n+(n﹣1)×n
=()+[]
=+
= ![]() ×
×
(3)实践应用:
通过以上探究过程,我们就可以算出当n为100时,正方形网格中正方形的总个数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com