
 如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为5.
如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为5. 科目:初中数学 来源: 题型:选择题
| A. | -2017 | B. | $\frac{1}{2017}$ | C. | 2017 | D. | $-\frac{1}{2017}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
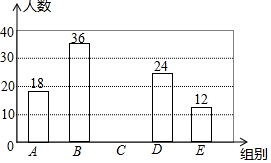 为了关注学生的身心健康发展,减轻学生的学业负担,某校对七年级学生完成家庭作业的时间进行问卷调查,随机抽取了部分学生,记录每个人平均每天完成家庭作业的时间,并将调查数据适当整理,绘制成如下两幅不完整的表和图:
为了关注学生的身心健康发展,减轻学生的学业负担,某校对七年级学生完成家庭作业的时间进行问卷调查,随机抽取了部分学生,记录每个人平均每天完成家庭作业的时间,并将调查数据适当整理,绘制成如下两幅不完整的表和图:| 组别 | 平均每天完成家庭作业的时间(x分钟) | 频数(人数) | 频率 |
| A | x≤40 | 18 | 0.15 |
| B | 40<x≤60 | a | b |
| C | 60<x≤80 | ||
| D | 80<x≤100 | 24 | 0.20 |
| E | x>100 | 12 | 0.10 |
| 合计 | c | 1.00 | |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | c<3 | B. | b<1 | C. | n≤2 | D. | m>$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
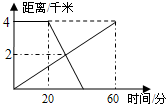 已知A,B两地相距4千米,上午8:00时,甲从A地步行到B地,8:20时乙从B地出发骑自行车到A地,甲、乙两人离A地的距离y(千米)与甲所用的时间x(分)之间的关系如图所示,则下列说法错误的是 ( )
已知A,B两地相距4千米,上午8:00时,甲从A地步行到B地,8:20时乙从B地出发骑自行车到A地,甲、乙两人离A地的距离y(千米)与甲所用的时间x(分)之间的关系如图所示,则下列说法错误的是 ( )| A. | 两人于8:30在途中相遇 | B. | 乙8:45到达A地 | ||
| C. | 甲步行的速度是4千米/时 | D. | 乙骑车的速度是$\frac{1}{5}$千米/分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
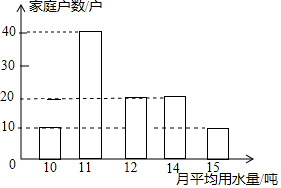 为了倡导“节约用水,从我做起”,市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果绘制成了如图所示的条形统计图,则这组数据的众数和中位数分别是( )
为了倡导“节约用水,从我做起”,市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果绘制成了如图所示的条形统计图,则这组数据的众数和中位数分别是( )| A. | 40,20 | B. | 11,11 | C. | 11,12 | D. | 11,11.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2,3 | B. | 3,4 | C. | 1,2 | D. | 0,1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | 1 | 1.1 | 1.2 | 1.3 | 1.4 |
| y | -1 | -0.49 | 0.04 | 0.59 | 1.16 |
| A. | 1 | B. | 1.1 | C. | 1.2 | D. | 1.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com