
| 实验的稻种数n∕粒 | 800 | 800 | 800 | 800 | 800 |
| 发芽的稻种数m∕粒 | 763 | 757 | 761 | 760 | 758 |
| 发芽的频率$\frac{m}{n}$ | 0.954 | 0.946 | 0.951 | 0.950 | 0.948 |
分析 利用频率估计概率得到随实验次数的增多,发芽的频率越来越稳定在0.95左右,由此可估计发芽的机会大约是0.95.
解答 解:根据表中的发芽的频率,当实验次数的增多时,发芽的频率越来越稳定在0.95左右,所以可估计这种大稻发芽的机会大约是0.95,
该农场播种了此稻种2万粒,那么能发芽的大约有0.95×2=1.9(万粒).
故答案为0.95;1.9.
点评 本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率;用频率估计概率得到的是近似值,随实验次数的增多,值越来越精确.


科目:初中数学 来源: 题型:解答题
 如图,已知四边形ABCD为⊙O的内接四边形,AE是⊙O的直径,连接BE、BD,P为⊙O外一点,连接PA,若∠AEB=40°,AE=12.
如图,已知四边形ABCD为⊙O的内接四边形,AE是⊙O的直径,连接BE、BD,P为⊙O外一点,连接PA,若∠AEB=40°,AE=12.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
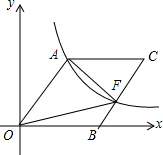 如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=$\frac{4}{5}$,反比例函数y=$\frac{48}{x}$在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于40.
如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=$\frac{4}{5}$,反比例函数y=$\frac{48}{x}$在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于40.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
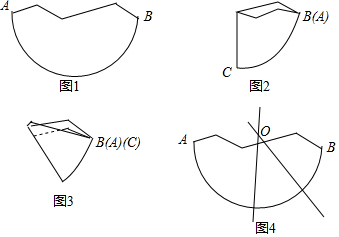 数学课上,老师介绍了利用尺规确定残缺纸片圆心的方法.小华对数学老师说:“我可以用拆叠纸片的方法确定圆心”.小华的作法如下:
数学课上,老师介绍了利用尺规确定残缺纸片圆心的方法.小华对数学老师说:“我可以用拆叠纸片的方法确定圆心”.小华的作法如下:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com