
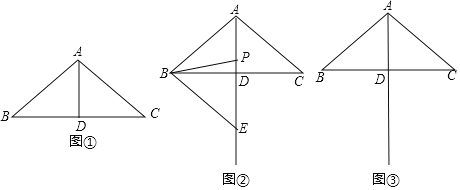
����Ŀ����ͼ�٣��ڡ�ABC�У�AB��AC��3����BAC��100����D��BC���е㣮
С����ͼ�ٽ���������̽�������߶�AD����ȡһ��P������PB�����߶�PB�Ƶ�P����ʱ�뷽����ת80������B�Ķ�Ӧ���ǵ�E������BE���õ���BPE��С�����֣����ŵ�P���߶�AD��λ�õı仯����E��λ��Ҳ�ڱ仯����E������ֱ��AD����࣬Ҳ������ֱ��AD�ϣ���������ֱ��AD���Ҳ࣮
�������С������̽����������������⣺
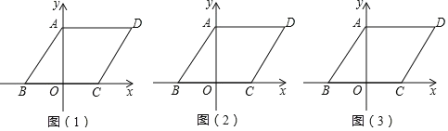
��1������E��ֱ��AD��ʱ����ͼ����ʾ��
�١�BEP���� ������
������CE��ֱ��CE��ֱ��AB��λ�ù�ϵ���� ����
��2������ͼ���л�����BPE��ʹ��E��ֱ��AD���Ҳ࣬����CE�����ж�ֱ��CE��ֱ��AB��λ�ù�ϵ����˵�����ɣ�
��3������P���߶�AD���˶�ʱ����AE����Сֵ��
���𰸡���1����50�㣻��AB��EC����2�������������3��3.
��������
��1���ٸ��ݡ�BPE=80�㣬PB=PE��������𰸣��ڸ��ݡ�AB��AC����BAC��100�㡱�����Եõ�AE��ֱƽ���߶�BC���Ӷ��õ�EB��EC�������õ���ECB����EBC������֤�á�ABC����ECB���Ӷ��õ��𰸣�
��2����PΪԲ�ģ�PBΪ�뾶����P���õ�PB��PC���ٸ���ͬ�����Ե�Բ�ܽ���Բ�ĵ�һ�������BCE�Ķ����Ӷ��õ��𰸣�
��3����AH��CE��H����E������CE���˶�����P���߶�AD���˶�������P�˶������A�غ�ʱ��AEȡ��Сֵ���ʶ��õ���.
�⣺��1������ͼ���У�
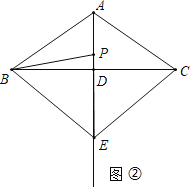
�ߡ�BPE��80�㣬PB��PE��
���PEB����PBE��50�㣬
�ڽ��ۣ�AB��EC��
���ɣ���AB��AC��BD��DC��
��AD��BC��
���BDE��90�㣬
���EBD��90�㩁50�㣽40�㣬
��AE��ֱƽ���߶�BC��
��EB��EC��
���ECB����EBC��40�㣬
��AB��AC����BAC��100�㣬
���ABC����ACB��40�㣬
���ABC����ECB��
��AB��EC��
�ʴ�Ϊ50��AB��EC��
��2����ͼ���У���PΪԲ�ģ�PBΪ�뾶����P��
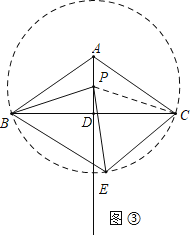
��AD��ֱƽ���߶�BC��
��PB��PC��
���BCE��![]() ��BPE��40�㣬
��BPE��40�㣬
�ߡ�ABC��40�㣬
��AB��EC��
��3����ͼ���У���AH��CE��H��
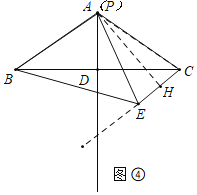
�ߵ�E������CE���˶�����P���߶�AD���˶���
�൱��P�˶������A�غ�ʱ��AE��ֵ��С����ʱAE����Сֵ��AB��3��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
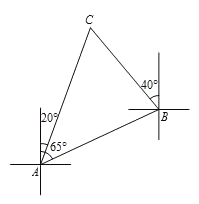
����Ŀ����ͼ��һ�Ҵ���A���ر�ƫ��65��������![]() km��B�ۣ�Ȼ�����ر�ƫ��40����������C�ۣ�C����A�۱�ƫ��20������.
km��B�ۣ�Ȼ�����ر�ƫ��40����������C�ۣ�C����A�۱�ƫ��20������.
��1����C�Ķ�����
��2��A��C����֮��ľ���Ϊ����km.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����⣺��1����ͼ�٣���Rt��ABC�У�AB��AC��DΪBC����һ�㣨�����B��C�غϣ������߶�AD�Ƶ�A��ʱ����ת90��õ�AE������EC�����߶�BC��DC��EC֮������ĵ�����ϵʽΪ�� ����
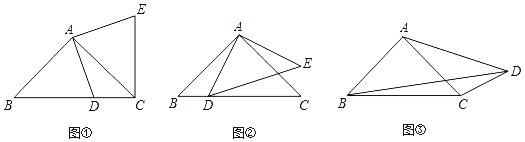
̽������2����ͼ�ڣ���Rt��ABC��Rt��ADE�У�AB��AC��AD��AE������ADE�Ƶ�A��ת��ʹ��D����BC���ϣ���̽���߶�AD��BD��CD֮������ĵ�����ϵ����֤����Ľ��ۣ�
Ӧ�ã���3����ͼ�ۣ����ı���ABCD�У���ABC����ACB����ADC��45�㣮��BD��9��CD��3����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
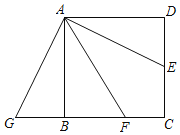
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4����E��CD���е㣬AFƽ����BAE��BC�ڵ�F������ADE�Ƶ�A˳ʱ����ת90������ABG����CF�ij�Ϊ____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
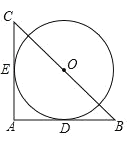
����Ŀ����ͼ���� Rt��ABC ��BC=2![]() ���� BC ���е� O ΪԲ�ĵġ�O �ֱ��� AB��AC ������ D��E ���㣬
���� BC ���е� O ΪԲ�ĵġ�O �ֱ��� AB��AC ������ D��E ���㣬![]() �ij�Ϊ�� ��
�ij��� ��
A.![]() B.
B.![]() C.��D.2��
C.��D.2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C����ABC��BE��AC������Ϊ��E����BDE�ǵȱ������Σ���AD��4�����߶�BE�ij�Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����Ӧ����̼��������ɫ�������Ĺ�����С�������������������г�ȥͼ��ݽ���.����ͬʱ�Ӽҳ�����С������150��/�ֵ��ٶ�����һ��ʱ�䣬��Ϣ��5���ӣ�����m��/���ӵ��ٶȵ���ͼ��ݣ�������ʼ����120��/���ӵ��ٶ����У�������ʻ��·��y���ף���ʱ��x�����ӣ��Ĺ�ϵ��ͼ������ͼ����������⣺
��1��ͼ��ݵ�С��ҵľ����� �ף�
��2��a= ��b= ��m= ��
��3��������ʻ��·��y���ף�����ʱ��x�����ӣ��ĺ�������ʽ�� ���������� .

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���ABCD��ƽ���ı��Σ�OB=OC=2��AB=![]() .
.
(1)���D�����ֱ꣬��CD�ĺ�������ʽ��
(2)��֪��P��ֱ��CD��һ�㣬����P����S��PAO=![]() S��ABOʱ�����P�����ꣻ
S��ABOʱ�����P�����ꣻ
(3)����M��ƽ��ֱ������ϵ�ڣ�����ֱ��AB���Ƿ���ڵ�F������A��B�غϣ���ʹ��A�� C�� F��MΪ������ı���Ϊ����?�����ڣ�ֱ��д��F������꣬�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ͬ�����������5�����ѵ�������˵ijɼ���ͼ��ʾ��

��1��������ɼ�������Ϊ ����������ɼ�����λ��Ϊ ����
��2��������������ɼ��ķ��
��3������ѵ���ɼ�������Ϊѡ����һ����Ա�������ã�Ϊʲô��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com