
【题目】如图,△ABC中,AB=AC=2,BC边上有10个不同的点 ![]() ,
, ![]() ,……
,…… ![]() , 记
, 记 ![]() (i = 1,2,……,10),那么
(i = 1,2,……,10),那么 ![]() 的值为( )
的值为( )
A.4
B.14
C.40
D.不能确定
【答案】C
【解析】解 : 过点A作AD⊥BC与D, 
在Rt△ABD和Rt△APiD中,
∵AB2=AD2+BD2,APi2=AD2+PiD2 ,
∴AB2APi2=AD2+BD2(AD2+PiD2)=BD2PiD2=(BD+PiD)(BDPiD)=PiCPiB,
∴APi2+PiCPiB=AB2=4,
∴Mi=4.
∴M1+M2+…+M10=4×10=40.
所以答案是 :40.
【考点精析】本题主要考查了等式和勾股定理的概念的相关知识点,需要掌握等式两边同时加上或减去或乘以或除以(不为0)一个代数式,所得结果仍是等式;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,不是定理的是( )
A. 直角三角形两锐角互余
B. 两直线平行,同旁内角互补
C. n边形的内角和为(n﹣2)×180°
D. 相等的角是对顶角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE=![]() ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
(1)当点P与点C重合时(如图1).求证:△BOG≌△POE;
(2)结合图2,通过观察、测量、猜想:![]() =______,并证明你的猜想;
=______,并证明你的猜想;
(3)把正方形ABCD改为菱形,其他条件不变(如图3),若AC=8,BD=6,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四个命题中是真命题的有( )
①同位角相等②相等的角是对顶角③直角三角形的两个锐角互余④三个内角相等的三角形是等边三角形⑤若|a|=|b|,则a2=b2.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正六边形ABCDEF的边长为6cm,P是对角线BE上一动点,过点P作直线l与BE垂直,动点P从B点出发且以1cm/s的速度匀速平移至E点.设直线l扫过正六边形ABCDEF区域的面积为S(cm2),点P的运动时间为t(s),下列能反映S与t之间函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 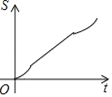
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com