练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．在一个不透明的袋子中装有2个红球，3个白球和4个黄球．这些球除颜色外其余均相同．从袋中随机摸出一个球，则摸到红球的概率是（　　）
    A．$\frac{7}{9}$B．$\frac{4}{9}$C．$\frac{1}{3}$D．$\frac{2}{9}$

    分析 先求出袋子中总的球数，再用红球的个数除以总的球数即可．

    解答 解：∵袋子中装有2个红球，3个白球和4个黄球，共有2+3+4=9个球，
    ∴从袋子中随机摸出一个球是红球的概率是$\frac{2}{9}$．
    故选：D．

    点评 此题考查了概率公式，如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=$\frac{m}{n}$．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    6．在△ABC中，用直尺和圆规作图（保留作图痕迹）．

    （1）如图①，在AC上作点D，使DB+DC=AC．
    （2）如图②，作△BCE，使∠BEC=∠BAC，CE=BE；
    （3）如图③，已知线段a，作△BCF，使∠BFC=∠A，BF+CF=a．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．网购越来越多地成为人们的一种消费方式，在2015年的“双11”促销活动中天猫和淘宝的支付交易额突破
    912.17亿元，将912.17亿元用科学记数法表示为（　　）
    A．912.17×108B．9.1217×108C．9.1217×109D．9.1217×1010

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．一枚质地均匀的正方体骰子的六个面分别刻有1到6的点数，将这枚骰子掷两次，其点数之和是7的概率为（　　）
    A．$\frac{1}{4}$B．$\frac{1}{5}$C．$\frac{1}{6}$D．$\frac{1}{7}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

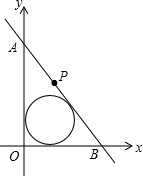    11．阅读理解：如果两个正数a，b，即a＞0，b＞0，有下面的不等式：$\frac{a+b}{2}$$≥\sqrt{ab}$，当且仅当a=b时取到等号我们把$\frac{a+b}{2}$叫做正数a，b的算术平均数，把$\sqrt{ab}$叫做正数a，b的几何平均数，于是上述不等式可表述为：两个正数的算术平均数不小于（即大于或等于）它们的几何平均数．它在数学中有广泛的应用，是解决最值问题的有力工具．
    初步探究：（1）已知x＞0，求函数y=x+$\frac{4}{x}$的最小值．
    问题迁移：（2）学校准备以围墙一面为斜边，用栅栏为成一个面积为100m2的直角三角形，作为英语角，直角三角形的两直角边各为多少时，所用栅栏最短？
    创新应用：（3）如图，在直角坐标系中，直线AB经点P（3，4），与坐标轴正半轴相交于A，B两点，当△AOB的面积最小时，求△AOB的内切圆的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．如图所示的图形是由7个完全相同的小正方形组成的立体图形，则这个立体图形的左视图是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．如图是由3个相同的正方体组成的一个立体图形，它的三视图是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图1，已知点E，F，G，H分别是四边形ABCD各边AB，BC，CD，DA的中点，根据以下思路可以证明四边形EFGH是平行四边形：
    （1）如图2，将图1中的点C移动至与点E重合的位置，F，G，H仍是BC，CD，DA的中点，求证：四边形CFGH是平行四边形；
    （2）如图3，在边长为1的小正方形组成的5×5网格中，点A，C，B都在格点上，在格点上画出点D，使点C与BC，CD，DA的中点F，G，H组成正方形CFGH；
    （3）在（2）条件下求出正方形CFGH的边长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．一司机驾驶汽车从甲地去乙地，他以平均80千米/小时的速度用了4个小时到达乙地，当他按原路匀速返回时．汽车的速度v千米/小时与时间t小时的函数关系是（　　）
    A．v=320tB．v=$\frac{320}{t}$C．v=20tD．v=$\frac{20}{t}$

    查看答案和解析>>

    同步练习册答案