
【题目】在平面直角坐标系xOy中,抛物线![]() 与y轴交于点A.
与y轴交于点A.
(1)直接写出点A的坐标;
(2)点A、B关于对称轴对称,求点B的坐标;
(3)已知点![]() ,
,![]() .若抛物线与线段PQ恰有两个公共点,结合函数图象,求a的取值范围.
.若抛物线与线段PQ恰有两个公共点,结合函数图象,求a的取值范围.
【答案】(1)(0,-3);(2)B(2,-3);(3) ![]() 或
或![]()
【解析】
(1)题干要求直接写出点A的坐标,将x=0代入即可求出;
(2)由题意知点A、B关于对称轴对称,求出对称轴从而即可求点B的坐标;
(3)结合函数图象,抛物线与线段PQ恰有两个公共点,分别对有两个公共点的情况进行讨论求解.
解:(1)由题意抛物线![]() 与y轴交于点A ,将x=0代入求出坐标为
与y轴交于点A ,将x=0代入求出坐标为![]() ;
;
(2)∵![]() ;
;
∴![]() .
.
(3)当抛物线过点P(4,0)时,![]() ,
,
∴![]() .
.
此时,抛物线与线段PQ有两个公共点.
当抛物线过点![]() 时,a=1,
时,a=1,
此时,抛物线与线段PQ有两个公共点.
∵抛物线与线段PQ恰有两个公共点,
∴![]() .
.
当抛物线开口向下时,![]() .
.
综上所述,当![]() 或
或![]() 时,抛物线与线段PQ恰有两个公共点.
时,抛物线与线段PQ恰有两个公共点.


科目:初中数学 来源: 题型:
【题目】某水果商店以5元/千克的价格购进一批水果进行销售,运输过程中质量耗5%,运输费用是0.7元/千克,假设不计其他费用
(1)商店要把水果售完至少定价为多少元才不会亏本?
(2)在销售过科中,商店发现每天荔枝的销售量m(千克)与销售单价x(元/千克)之间满足关系m=﹣10x+120,那么当销售单价定为多少时,每天获得的利润w最大?
(3)该商店决定每销售一千克水果就捐赠a元利润(a≥1)给希望工程,通过销售记录发现,销侮价格大于每千克11元时,扣除捐赠后每天的利润随x增大而减小,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
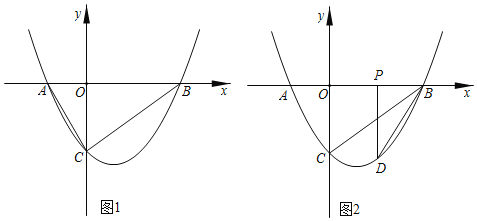
如图1,抛物线y=ax2+bx﹣3与x轴交于A(﹣2,0),B(4,0)两点,与y轴交于点C.
(1)求抛物线的表达式;
(2)点N是抛物线上异于点C的动点,若△NAB的面积与△CAB的面积相等,求出点N的坐标;
(3)如图2,当P为OB的中点时,过点P作PD⊥x轴,交抛物线于点D.连接BD,将△PBD沿x轴向左平移m个单位长度(0<m≤2),将平移过程中△PBD与△OBC重叠部分的面积记为S,求S与m的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
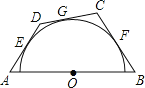
【题目】如图,AB是定长线段,圆心O是AB的中点,AE、BF为切线,E、F为切点,满足AE=BF在![]() 上取动点G,过点G作切线交AE、BF的延长线于点D、C,当点G运动时,设AD=y,BC=x,则y与x所满足的函数关系式为( )
上取动点G,过点G作切线交AE、BF的延长线于点D、C,当点G运动时,设AD=y,BC=x,则y与x所满足的函数关系式为( )
A.正比例函数y=kx(k为常数,k≠0,x>0)B.一次函数y=kx+b(k,b为常数,kb≠0,x>0)
C.二次函数y=ax2+bx+c(a,b,c为常数,a≠0,x>0)D.以上都不是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c开口向上,与x轴交于点A、B,与y轴交于点C
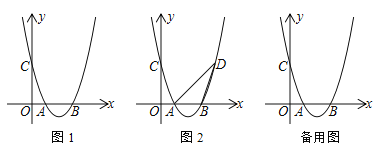
(1) 如图1,若A (1,0)、C (0,3)且对称轴为直线x=2,求抛物线的解析式
(2) 在(1)的条件下,如图2,作点C关于抛物线对称轴的对称点D,连接AD、BD,在抛物线上是否存在点P,使∠PAD=∠ADB,若存在,求出点P的坐标,若不存在,请说明理由
(3) 若直线l:y=mx+n与抛物线有两个交点M、N(M在N的左边),Q为抛物线上一点(不与M、N重合),过点Q作QH平行于y轴交直线l于点H,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
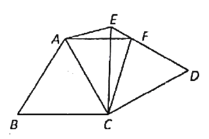
【题目】如图,将等边△ABC绕点C顺时针旋转90得到△DEC,∠ACD的平分线CF交DE于点F,连接AE,AF.
(1)求∠CEA度数;
(2)求证AF⊥CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“大美武汉·诗意江城”,某校数学兴趣小组就“最想去的武汉市旅游景点”随机调查了本校3000名学生中的部分学生,提供四个景点选择:A、黄鹤楼;B、东湖海洋世界;C、极地海洋世界;D、欢乐谷.要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:
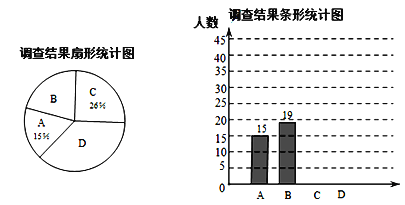
请根据图中提供的信息,解答下列问题:
(1) 一共调查了学生___________人
(2) 扇形统计图中表示“最想去的景点D”的扇形圆心角为___________度
(3) 如果A、B、C、D四个景点提供给学生优惠门票价格分别为20元、30元、40元、60元,根据以上的统计估计全校学生到对应的景点所需要门票总价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,点
中,点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() .
.
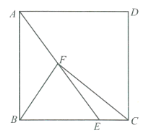

图1 图2
(1)如图1,点![]() 为
为![]() 的中点,连接
的中点,连接![]() .已知
.已知![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)如图2,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 为对角线
为对角线![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com