
【题目】如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
(1)若∠AOB=60,OM=4,OQ=1,求证:CN⊥OB.
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问: ![]() 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.

②设菱形OMPQ的面积为S1,△NOC的面积为S2,求![]() 的取值范围.
的取值范围.
【答案】(1)CN⊥OB;(2)①![]() ②0<
②0<![]() ≤
≤![]()
【解析】试题分析:(1)过P作PE⊥OA于E,易证四边形OMPQ为平行四边形.根据三角函数求得PE的长,再根据三角函数求得∠PCE的度数,即可得∠CPM=90,又因PM∥OB,即可证明CN⊥OB.(2)①设OM=x,ON=y,先证△NQP∽△NOC,即可得![]() ,把x,y代入整理即可得
,把x,y代入整理即可得![]() -
-![]() 的值.②过P作PE⊥OA于E,过N作NF⊥OA于F,可得S1=OM·PE,S2=
的值.②过P作PE⊥OA于E,过N作NF⊥OA于F,可得S1=OM·PE,S2=![]() OC·NF,所以
OC·NF,所以![]() =
=![]() .再证△CPM∽△CNO,所以
.再证△CPM∽△CNO,所以![]() =
=![]() =
=![]() ,用x表示出
,用x表示出![]() 与x的关系,根据二次函数的性质即可得
与x的关系,根据二次函数的性质即可得![]() 的取值范围.
的取值范围.
试题解析:(1)
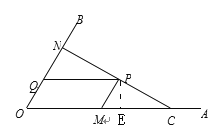
过P作PE⊥OA于E.∵PQ∥OA,PM∥OB,∴四边形OMPQ为平行四边形.
∴PM=OQ=1,∠PME=∠AOB=60,
∴PE=PM·sin60=![]() ,ME=
,ME=![]() ,
,
∴CE=OC-OM-ME=![]() ,∴tan∠PCE=
,∴tan∠PCE=![]() =
=![]() ,
,
∴∠PCE=30,∴∠CPM=90,
又∵PM∥OB,/span>∴∠CNO=∠CPM=90 ,即CN⊥OB.
(2)①![]() -
-![]() 的值不发生变化. 理由如下:
的值不发生变化. 理由如下:
设OM=x,ON=y.∵四边形OMPQ为菱形,∴ OQ=QP=OM=x,NQ=y-x.
∵PQ∥OA,∴∠NQP=∠O.又∵∠QNP=∠ONC,∴△NQP∽△NOC,∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴6y-6x=xy.两边都除以6xy,得![]() -
-![]() =
=![]() ,即
,即![]() -
-![]() =
=![]() .
.
②过P作PE⊥OA于E,过N作NF⊥OA于F,
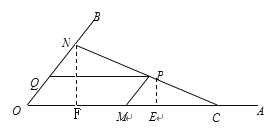
则S1=OM·PE,S2=![]() OC·NF,
OC·NF,
∴![]() =
=![]() .
.
∵PM∥OB,∴∠MCP=∠O.又∵∠PCM=∠NCO,
∴△CPM∽△CNO.∴![]() =
=![]() =
=![]() .
.
∴![]() =
=![]() =-
=-![]() (x-3)2+
(x-3)2+![]() .
.
∵0<x<6,由这个二次函数的图像可知,0<![]() ≤
≤![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,AT是⊙O的切线,∠ABT=50°,BT交⊙O于点C,E是AB上一点,延长CE交⊙O于点D.
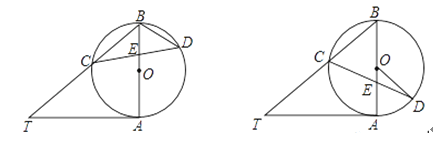
(1)如图①,求∠T和∠CDB的大小;
(2)如图②,当BE=BC,求∠CDO的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
如图1,已知线段AB、CD相交于点O,且AB=CD,请你利用所学知识把线段AB、CD转移到同一三角形中。
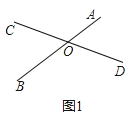
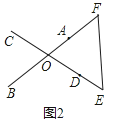
小强同学利用平移知识解决了此问题,具体做法如下:
如图2,延长OD至点E,使DE=CO,延长OA至点F,使AF=OB,连接EF,则△OEF为所求的三角形。
请你仔细体会小强的做法,探究并解答下列问题:
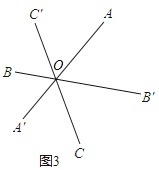
如图3,长为2的三条线段AA′,BB′,CC′交于一点O,并且∠B′OA=∠C′OB=∠A′OC=60°;
(1)请你把三条线段AA′,BB′,CC′ 转移到同一三角形中。(简要叙述画法)
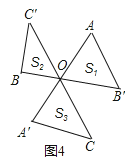
(2)连接AB′、BC′、CA′,如图4,设△AB′O、△BC′O、△CA′O的面积分别为S1、S2、S3,则S1+S2+S3________(填“>”或“<”或“=”)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结沦中,错误的有( )
①Rt△ABC中,已知两边分别为3和4,则第三边的长为5;②三角形的三边分别为a、b、c,若a2+b2=c2,则∠A=90°;③若△ABC中,∠A:∠B:∠C=1:5:6,则这个三角形是一个直角三角形;④若(x﹣y)2+M=(x+y)2成立,则M=4xy.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
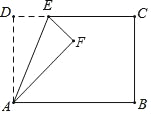
【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD的边AD在y轴上,抛物线![]() 经过点A、点B,与x轴交于点E、点F,且其顶点M在CD上。
经过点A、点B,与x轴交于点E、点F,且其顶点M在CD上。
(1)请直接写出下列各点的坐标:
A ,B ,C ,D ;
(2)若点P是抛物线上一动点(点P不与点A、点B重合),过点P作![]() 轴的平行线l与直线AB交于点G,与直线BD交于点H,如图2。
轴的平行线l与直线AB交于点G,与直线BD交于点H,如图2。
①当线段PH=2GH时,求点P的坐标;
②当点P在直线BD下方时,点K在直线BD上,且满足△KPH∽△AEF,求△KPH面积的最大值。
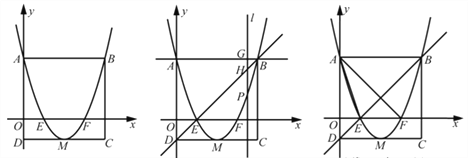
图1 图2 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面内,两条直线L1,L2相交于点O,对于平面内任意一点M,若p,q分别是点M到直线L1,L2的距离,则称(p,q)为点M的“距离坐标”.根据上述规定,“距离坐标”是(2,1)的点共有_____个

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接元旦,孝昌县政府要在广场上设计一座三角形展台,要求园林工人把它的每条边上摆放上相等盆数的盆栽鲜花(如图所示的每个小圆圈表示一盆鲜花)以美化环境,如果每条边上摆放两盆鲜花,共需要3盆鲜花;如果每条边上摆放3盆鲜花,共需要6盆鲜花;…,按此要求摆放下去:

(1)根据图示填写下表:
每条边上摆放的盆数( | 2 | 3 | 4 | 5 | 6 | … |
共需要的盆数( | 3 | 6 | … |
(2)如果要在每条边上摆放![]() 盆鲜花,那么需要鲜花的总盆数 .
盆鲜花,那么需要鲜花的总盆数 .
(3)请你帮园林工人参考一下,能否用2020盆鲜花作出符合要求的摆放?如果能,请计算出每条边上应摆放花的盆数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一串图形按如图所示的规律排列.

(说明:下列所指的小正方形都是与第1个图形一样大小的正方形)
(1)第5个图形中有几个小正方形?第6个图形呢?
(2)求出第![]() 个图形中小正方形的个数.
个图形中小正方形的个数.
(3)求出第20个图形中小正方形的个数.
(4)是否存在某个图形,其小正方形的个数恰好是下列各数:① 5050;②1000.给出你的判断,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com