练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图所示的网格图均是20×20的等距网格图（每个小方格的边长均为1个单位长）．侦察兵王凯在点P处观察区域MNCD内的活动情况，当5个单位长的列车AB（图中的-）以每秒1个单位长的速度在铁路线MN上通过时，列车将阻挡王凯的部分视线，在区域MNCD内形成盲区（不考虑列车的宽度和车厢间的缝隙）．请针对图①，②，③中列车位于不同位置的情形分别画出相应的盲区，并在盲区内涂上阴影．
    考点：视点、视角和盲区
    专题：
    分析：根据盲区的定义，分别得出在区域MNCD内形成盲区即可．
    解答：解：如图所示：
    点评：此题主要考查了盲区的定义，正确把握盲区的定义是解题关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    若b是a和c的比例中项，c是b和d的比例中项，下列各式不一定成立的是（　　）
    A、
    a
    b
    =
    b
    c
    B、
    a
    d
    =
    b
    c
    C、
    b
    c
    =
    c
    d
    D、
    a
    b
    =
    c
    d

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知一个圆锥沿轴剖开是一个等腰三角形．若这个三角形的底为8cm，腰为10cm．
    （1）求圆锥侧面展开图的扇形弧长；
    （2）求圆锥的表面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

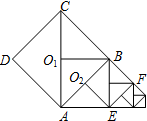    如图，以边长为1的正方形ABCD的边AB为对角线作第二个正方形AEBO1，再以BE为对角线作第三个正方形EFBO2，如此作下去…则所作的第2013个正方形的面积是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

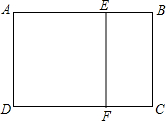    如果一个矩形的宽与长的比是黄金比，那么这个矩形称为黄金矩形．如图，已知四边形ABCD为黄金矩形，以它的宽为边在其内部作正方形AEFD，那么剩下的矩形BCFE也是一个黄金矩形，你能证明这个结论吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    一个梯形，它的下底比上底长2cm，它的高为3cm，设它的上底长为xcm，它的面积为y cm2．
    （1）写出y与x之间的关系式，并指出哪个变量是自变量，哪个变量是因变量．
    （2）当x由5cm变到7cm时，y如何变化？
    （3）用表格表示当x从3cm变到10cm时（每次增加1cm），y的相应值．
    （4）当x每增加1cm时，y如何变化？说明理由．
    （5）这个梯形的面积能等于9cm2吗？能等于2cm2吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某厂从2010年开始投入技改资金，经技术改进后，其产品的生产成本不断降低，具体数据如下表：
    年度 2010 2011 2012 2013
    投入技改资金x（万元） 2.5 3 4 4.5
    产品成本y（万元/件） 7.2 6 4.5 4
    请你认真分析表中数据，从你所学习过的一次函数和反比例函数中确定一种函数来表示其变化规律，说明确定是这种函数而不是另一种函数的理由，并求出它的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    抛物线y=ax2（a≠0）与直线y=4x-3交于点A（m，1）．
    （1）求点A的坐标及抛物线的解析式；
    （2）写出抛物线的开口方向、顶点坐标和对称轴；
    （3）写出抛物线y=ax2与直线y=4x-3的另一个交点B的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，AB⊥BC，DC⊥BC，若∠DBC=45°，∠A=70°，求∠D，∠AED，∠BFE的度数．

    查看答案和解析>>

    同步练习册答案