
【题目】已知,![]() 内接于
内接于![]() ,点
,点![]() 是弧
是弧![]() 的中点,连接
的中点,连接![]() 、
、![]() ;
;
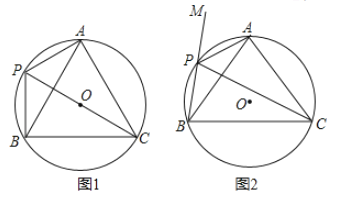
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)见解析;(3)2![]() .
.
【解析】
(1)由点P是弧AB的中点,可得出AP=BP, 通过证明![]() ,
,![]() 可得出
可得出![]() 进而证明AB
进而证明AB![]() PC.
PC.
(2)由PA是∠CPM的角平分线,得到∠MPA=∠APC, 等量代换得到∠ABC=∠ACB, 根据等腰三角形的判定定理即可证得AB=AC.
(3)过A点作AD⊥BC,有三线合一可知AD平分BC,点O在AD上,连结OB,则∠BOD=∠BAC,根据圆周角定理可知∠BOD=∠BAC, ∠BPC=∠BAC,由∠BOD=∠BPC可得 ![]() ,设OB=
,设OB=![]() ,根据勾股定理可算出OB、BD、OD、AD的长,再次利用勾股定理即可求得AP的值.
,根据勾股定理可算出OB、BD、OD、AD的长,再次利用勾股定理即可求得AP的值.
解:(1)∵点P是弧AB的中点,如图1,
∴AP=BP,
在△APC和△BPC中
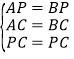 ,
,
∴△APC≌△BPC(SSS),
∴∠ACP=∠BCP,
在△ACE和△BCE中
 ,
,
∴△ACE≌△BCE(SAS),
∴∠AEC=∠BEC,
∵∠AEC+∠BEC=180°,
∴∠AEC=90°,
∴AB⊥PC;
(2)∵PA平分∠CPM,
∴∠MPA=∠APC,
∵∠APC+∠BPC+∠ACB=180°,∠MPA+∠APC+∠BPC=180°,
∴∠ACB=∠MPA=∠APC,
∵∠APC=∠ABC,
∴∠ABC=∠ACB,
∴AB=AC;
(3)过A点作AD⊥BC交BC于D,连结OP交AB于E,如图2,

由(2)得出AB=AC,
∴AD平分BC,
∴点O在AD上,
连结OB,则∠BOD=∠BAC,
∵∠BPC=∠BAC,
∴![]() =
=![]() ,
,
设OB=25x,则BD=24x,
∴OD=![]() =7x,
=7x,
在![]() 中,AD=25x+7x=32x,BD=24x,
中,AD=25x+7x=32x,BD=24x,
∴AB=![]() =40x,
=40x,
∵AC=8,
∴AB=40x=8,
解得:x=0.2,
∴OB=5,BD=4.8,OD=1.4,AD=6.4,
∵点P是![]() 的中点,
的中点,
∴OP垂直平分AB,
∴AE=![]() AB=4,∠AEP=∠AEO=90°,
AB=4,∠AEP=∠AEO=90°,
在![]() 中,OE=
中,OE=![]() ,
,
∴PE=OP﹣OE=5﹣3=2,
在![]() 中,AP=
中,AP=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,某公路检测中心在一事故多发地带安装了一个测速仪,检测点设在距离公路10m的A处,测得一辆汽车从B处行驶到C处所用的时间为0.9秒.已知∠B=30°,∠C=45°

(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,羊年春节到了,小明亲手制作了![]() 张一样的卡片,在每张卡片上分别写上“新”“年”“好”三个字,并随机放入一个不透明的信封中,然后让小芳分三次从信封中摸
张一样的卡片,在每张卡片上分别写上“新”“年”“好”三个字,并随机放入一个不透明的信封中,然后让小芳分三次从信封中摸![]() 张卡片(每次摸
张卡片(每次摸![]() 张,摸出不放回).
张,摸出不放回).
![]()
![]() 小芳第一次抽取的卡片是“新”字的概率是多少?
小芳第一次抽取的卡片是“新”字的概率是多少?
![]() 请通过画树状图或列表,求小芳先后抽取的
请通过画树状图或列表,求小芳先后抽取的![]() 张卡片分别是“新年好”的概率.
张卡片分别是“新年好”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 于点H,点D在AH上,且
于点H,点D在AH上,且![]() ,连接BD.
,连接BD.
![]() 如图1,将
如图1,将![]() 绕点H旋转,得到
绕点H旋转,得到![]() 点B、D分别与点E、F对应
点B、D分别与点E、F对应![]() ,连接AE,当点F落在AC上时
,连接AE,当点F落在AC上时![]() 不与C重合
不与C重合![]() ,求AE的长;
,求AE的长;
![]() 如图2,
如图2,![]() 是由
是由![]() 绕点H逆时针旋转
绕点H逆时针旋转![]() 得到的,射线CF与AE相交于点G,连接GH,试探究线段GH与EF之间满足的等量关系,并说明理由.
得到的,射线CF与AE相交于点G,连接GH,试探究线段GH与EF之间满足的等量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在Rt△ABC中,∠B=90°,BC=4cm,AB=8cm,D、E、F分别为AB、AC、BC边上的中点.若P为AB边上的一个动点,PQ∥BC,且交AC于点Q,以PQ为一边,在点A的异侧作正方形PQMN,记正方形PQMN与矩形EDBF的公共部分的面积为y.
(1)如图,当AP=3cm时,求y的值;
(2)设AP=xcm,试用含x的代数式表示y(cm2);
(3)当y=2cm2时,试确定点P的位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
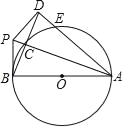
【题目】如图,AB是⊙O的直径,点D是⊙O外一点,AB=AD,BD交⊙O于点C,AD交⊙O于点E,点P是AC的延长线上一点,连接PB、PD,且PD⊥AD
(1)判断PB与⊙O的位置关系,并说明理由;
(2)连接CE,若CE=3,AE=7,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
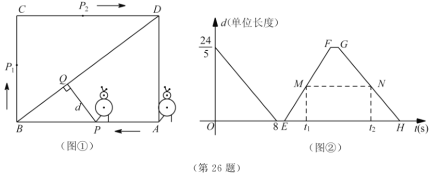
【题目】某校机器人兴趣小组在如图①所示的矩形场地上开展训练.机器人从点![]() 出发,在矩形
出发,在矩形![]() 边上沿着
边上沿着![]() 的方向匀速移动,到达点
的方向匀速移动,到达点![]() 时停止移动.已知机器人的速度为
时停止移动.已知机器人的速度为![]() 个单位长度/
个单位长度/![]() ,移动至拐角处调整方向需要
,移动至拐角处调整方向需要![]()
![]() (即在
(即在![]() 、
、![]() 处拐弯时分别用时
处拐弯时分别用时![]()
![]() ).设机器人所用时间为
).设机器人所用时间为![]() 时,其所在位置用点
时,其所在位置用点![]() 表示,
表示,![]() 到对角线
到对角线![]() 的距离(即垂线段
的距离(即垂线段![]() 的长)为
的长)为![]() 个单位长度,其中
个单位长度,其中![]() 与
与![]() 的函数图像如图②所示.
的函数图像如图②所示.
(1)求![]() 、
、![]() 的长;
的长;
(2)如图②,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,线段
上,线段![]() 平行于横轴,
平行于横轴,![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() 、
、![]() .设机器人用了
.设机器人用了![]() 到达点
到达点![]() 处,用了
处,用了![]() 到达点
到达点![]() 处(见图①).若
处(见图①).若![]() ,求
,求![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
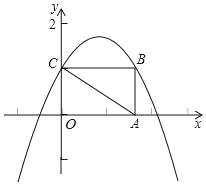
【题目】如图,平面直角坐标系xOy中,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,且点C的坐标是(0,1),点B的坐标是(![]() ,1),抛物线y=﹣x2+bx+c经过点B和点C.
,1),抛物线y=﹣x2+bx+c经过点B和点C.
(1)求抛物线y=﹣x2+bx+c的表达式:
(2)将△OAC沿直线AC折叠,点O的对称点记为点D,请判断:点D是否在抛物线上?并说明理由;
(3)点E为线段AC上的一个动点.
①若点P在抛物线上,其横坐标为m,当PE⊥AC且PE=![]() 时.请直接写出m的值;
时.请直接写出m的值;
②若点F为线段AB上一个动点,且CE=AF,当OE+OF的值最小时,请直接写出点F的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com