

分析 (1)证出l∥BC,得出比例式$\frac{AM}{AB}=\frac{AN}{AC}$,证出AM=AN,得出ME=NE,因此MN=2AE=2t,证出MN=BP,即可得出四边形MBPN为平行四边形;
(2)由正方形的性质得出FG=MN=MF=2AE=2t,求出DH=AD-AH=10-3t,得出S△PFG=$\frac{1}{2}$FG•DH=-3(t-$\frac{5}{3}$)2+$\frac{25}{3}$,由二次函数的最值即可得出答案;
(3)利用勾股定理得:PF2=2(10-3t)2,PG2=(10-3t)2+(10-t)2,FG2=(2t)2,分三种情况讨论,得出方程,解方程即可.
解答 (1)证明:∵l⊥AD,BC⊥AD,
∴l∥BC,
∴$\frac{AM}{AB}=\frac{AN}{AC}$,
∵AB=AC,
∴AM=AN,∵∠BAC=90°,
∴ME=NE,
∴MN=2AE=2t,
∵BP=2t,
∴MN=BP,
∴四边形MBPN为平行四边形;
(2)解:∵四边形MFGN是正方形,
∴FG=MN=MF=2AE=2t,
∵EH=MF=2t,
∴DH=AD-AH=10-3t,
∴S△PFG=$\frac{1}{2}$FG•DH=$\frac{1}{2}$×2t×(10-3t)=-3(t-$\frac{5}{3}$)2+$\frac{25}{3}$,
∵a=-3<0,0<t<$\frac{10}{3}$,
∴当t=$\frac{5}{3}$时,S△PFG最大=$\frac{25}{3}$;
(3)解:存在,当t=$\frac{30±10\sqrt{2}}{7}$或t=5或t=10时,△PFG为等腰三角形;理由如下:
利用勾股定理得:PF2=2(10-3t)2,PG2=(10-3t)2+(10-t)2,又FG2=(2t)2,
当PF=FG时,则2(10-3t)2=(2t)2,
解得:t=$\frac{30±10\sqrt{2}}{7}$,
当PF=PG时,2(10-3t)2=(10-3t)2+(10-t)2,
解得:t=5,或t=0(舍去);
当FG=PG时,(2t)2=(10-3t)2+(10-t)2,
解得:t=10,或t=$\frac{10}{3}$(舍去);
综上所述,t=$\frac{30±10\sqrt{2}}{7}$或t=5或t=10时,△PFG为等腰三角形.
点评 本题是四边形综合题目,考查了平行四边形的判定、正方形的性质、等腰三角形的判定、二次函数的最值、勾股定理等知识;本题综合性强,难度较大.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 学校举行“文明环保,从我做起”征文比赛.现有甲班上交40篇作文,乙班上交30篇作文,现将两班的作文的成绩(单位:分)统计如下:
学校举行“文明环保,从我做起”征文比赛.现有甲班上交40篇作文,乙班上交30篇作文,现将两班的作文的成绩(单位:分)统计如下:| 等级 | 成绩(S) | 频数 |
| A | 90<S≤100 | x |
| B | 80<S≤90 | 16 |
| C | 70<S≤80 | 18 |
| D | S≤70 | 3 |
| 合计 | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12×105 | B. | 1.2×106 | C. | 1.2×105 | D. | 0.12×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
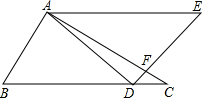 将一副三角板拼成如图所示的图形,即∠BAC=∠ADE=90°,∠DAE=∠E=45°,∠C=30°,∠B=60°,DE与AC相交于点F.
将一副三角板拼成如图所示的图形,即∠BAC=∠ADE=90°,∠DAE=∠E=45°,∠C=30°,∠B=60°,DE与AC相交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com