
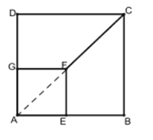
【题目】(1)如图①,正方形![]() 的两边分别在正方形
的两边分别在正方形![]() 的边
的边![]() 和
和![]() 上,连接
上,连接![]() .填空:线段
.填空:线段![]() 与
与![]() 的数量关系为________;直线
的数量关系为________;直线![]() 与
与![]() 所夹锐角的大小为________.
所夹锐角的大小为________.



(2)如图②,将正方形![]() 绕点
绕点![]() 顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.
顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.
(3)把图②中的正方形都换成菱形,且![]() ,如图③,直接写出
,如图③,直接写出![]() ______.
______.
【答案】(1)①![]() ,②45°;(2)仍然成立,见解析;(3)
,②45°;(2)仍然成立,见解析;(3)![]()
【解析】
(1)根据正方形的性质即可得出答案;
(2)过![]() 作
作![]() ,且
,且![]() ,连接
,连接![]() ,
,![]() ,并延长交
,并延长交![]() 、
、![]() 交于点
交于点![]() ,证明
,证明![]() ,接着证明四边形
,接着证明四边形![]() 是平行四边形,即可得出答案;
是平行四边形,即可得出答案;
(3)过![]() 作∠GDH=120°,且
作∠GDH=120°,且![]() ,连接
,连接![]() ,
,![]() ,证明
,证明![]() ,接着证明四边形
,接着证明四边形![]() 是平行四边形,再过点D作DM⊥GH于点M,证出GM=
是平行四边形,再过点D作DM⊥GH于点M,证出GM=![]() GH=
GH=![]() CF,DM=
CF,DM=![]() DG,再利用勾股定理计算即可得出答案.
DG,再利用勾股定理计算即可得出答案.
解:(1)①线段![]() 与
与![]() 的数量关系为
的数量关系为![]() ;
;
②直线![]() 与
与![]() 所夹锐角的度数为45°.
所夹锐角的度数为45°.
连接AF,根据正方形的性质可得A、F、C三点共线,∠CAD=45°
∵AF=![]() AG,AC=
AG,AC=![]() AD
AD
∴CF=AC-AF=![]() (AD-AG)=
(AD-AG)=![]() DG
DG
(2)仍然成立,证明如下:
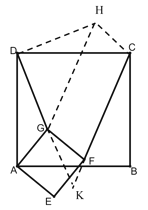
过![]() 作
作![]() ,且
,且![]() ,连接
,连接![]() ,
,![]() ,并延长交
,并延长交![]() 、
、![]() 交于点
交于点![]()
∵四边形![]() 是正方形
是正方形
∴![]() ,
,![]()
∵![]()
∴![]()
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,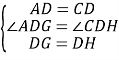
∴![]() ,
,
∴![]() ,
,![]()
∵四边形![]() 是正方形
是正方形
∴![]() ,
,![]() ,∴
,∴![]()
∵![]() ,
,![]()
∴![]()
∴![]() ,
,
![]() ,
,
∴![]()
∴![]()
∴四边形![]() 是平行四边形
是平行四边形
∴![]() ,
,![]()
在![]() 中,
中,![]()
∴![]() ,
,
即![]() ,
,
∵![]()
∴![]() ,即直线
,即直线![]() 与
与![]() 所夹锐角的度数为45°;
所夹锐角的度数为45°;
(3)过![]() 作∠GDH=120°,且
作∠GDH=120°,且![]() ,连接
,连接![]() ,
,![]()
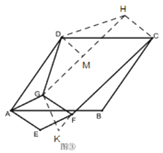
∵四边形![]() 是菱形 ,
是菱形 ,![]()
∴![]() ,∠ADC=120°
,∠ADC=120°
∵∠GDH=120°
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,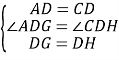
∴![]() ,
,
∴![]() ,
,![]()
∵四边形![]() 是菱形
是菱形
∴![]() ,
,![]() ,
,
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]() ,
,
![]() ,
,
∴![]()
∴![]()
∴四边形![]() 是平行四边形
是平行四边形
∴![]() ,
,![]()
过点D作DM⊥GH于点M
∴GM=![]() GH=
GH=![]() CF,DM=
CF,DM=![]() DG
DG
在Rt△DGM中,![]()
∴GM=![]() DG,
DG,
∴DG:CF=![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】某化妆品店老板到厂家选购A、B两种品牌的化妆品,若购进A品牌的化妆品5套,B品牌的化妆品6套,需要950元;若购进A品牌的化妆品3套,B品牌的化妆品2套,需要450元.
![]() 求A、B两种品牌的化妆品每套进价分别为多少元?
求A、B两种品牌的化妆品每套进价分别为多少元?
![]() 若销售1套A品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套,且B品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货?
若销售1套A品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套,且B品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABC中,AB=AC=6![]() ,∠BAC=90°,点D、E为BC边上的两点,分别沿AD、AE折叠,B、C两点重合于点F,若DE=5,则AD的长为_____.
,∠BAC=90°,点D、E为BC边上的两点,分别沿AD、AE折叠,B、C两点重合于点F,若DE=5,则AD的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题:已知:如图,![]() ,
,![]() .求证:
.求证:![]() .
.

老师要求学生在完成这道教材上的题目证明后,尝试对图形进行变形,继续做拓展探究,看看有什么新发现?
(1)小颖首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小颖用到的平行线性质可能是 .
(2)接下来,小颖用《几何画板》对图形进行了变式,她先画了两条平行线![]() ,然后在平行线间画了一点
,然后在平行线间画了一点![]() ,连接
,连接![]() 后,用鼠标拖动点
后,用鼠标拖动点![]() ,分别得到了图
,分别得到了图![]()
![]() ,小颖发现图
,小颖发现图![]() 正是上面题目的原型,于是她由上题的结论猜想到图
正是上面题目的原型,于是她由上题的结论猜想到图![]() 和
和![]() 图中的与
图中的与![]() 之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
之间也可能存在着某种数量关系.于是她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
请你在小颖操作探究的基础上,继续完成下面的问题:
(ⅰ)猜想图![]() 中
中![]() 与
与![]() 之间的数量关系并加以证明;
之间的数量关系并加以证明;
(ⅱ)补全图![]() ,直接写出
,直接写出![]() 与
与![]() 之间的数量关系: .
之间的数量关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中,如图(2).


求(1)抛物线的解析式;
(2)两盏景观灯P1、P2之间的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 从
从![]() 出发,以每秒1个单位的速度沿射线
出发,以每秒1个单位的速度沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() .
.


(1)当![]() 时.
时.
①如图2.当点![]() 落在
落在![]() 上时,显然
上时,显然![]() 是直角三角形,求此时
是直角三角形,求此时![]() 的值;
的值;
②当点![]() 不落在
不落在![]() 上时,请直接写出
上时,请直接写出![]() 是直角三角形时
是直角三角形时![]() 的值;
的值;
(2)若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,且当
,且当![]() 时,
时,![]() .问:当
.问:当![]() ,
,![]() 的大小是否发生变化,若不变,请说明理由.
的大小是否发生变化,若不变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,于点E

(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小王某天下午营运是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:
+15,-2,+5,-1,+10,-3,-2,+12,+4,-5,+6.
(1)将最后一名乘客送到目的地时,小王距下午出车时的出发点多远?
(2)若汽车耗油量为0.05升/千米,这天下午小王的汽车共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形一腰上的高与另一腰的夹角为 45°,则这个等腰三角形的底角为( )
A.67°B.67.5°C.22.5°D.67.5°或 22.5°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com