
| 类 别 | 电视机 | 洗衣机 |
| 进价(元/台) | 1 800 | 1 500 |
| 售价(元/台) | 2 000 | 1 600 |
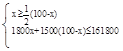
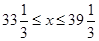


科目:初中数学 来源:不详 题型:解答题
 是等边三角形,点
是等边三角形,点 坐标为(-8,0)、点
坐标为(-8,0)、点 坐标为(8,0),点
坐标为(8,0),点 在
在 轴的正半轴上.一条动直线从
轴的正半轴上.一条动直线从 轴出发,以每秒1个单位长度的速度沿
轴出发,以每秒1个单位长度的速度沿 轴向右平移,直线与直线
轴向右平移,直线与直线 交于点
交于点 ,与线段
,与线段 交于点
交于点 .以
.以 为边向左侧作等边△
为边向左侧作等边△ ,
, 与
与 轴的交点为
轴的交点为 .当点
.当点 与点
与点 重合时,直线停止运动,设直线的运动时间为(秒).
重合时,直线停止运动,设直线的运动时间为(秒).
 的坐标为 ,四边形
的坐标为 ,四边形 的形状一定是 ;
的形状一定是 ; 能不能是菱形?若能,求出相应的的值;若不能,请说明理由.
能不能是菱形?若能,求出相应的的值;若不能,请说明理由. 恰好落在以
恰好落在以 为直径的⊙
为直径的⊙ 上?并求出此时⊙
上?并求出此时⊙ 的半径.
的半径.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象上的一点.
的图象上的一点.
 与双曲线
与双曲线 的两个交点分别为P和P′,
的两个交点分别为P和P′, <
< 时,直接写出x的取值范围.
时,直接写出x的取值范围.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.(30,30) | B.(﹣8 ,8 ,8 ) ) | C.(﹣4 ,4 ,4 ) ) | D.(4 ,﹣4 ,﹣4 ) ) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
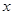 分钟,上网费用为
分钟,上网费用为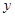 元.
元.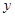 元与上网时间
元与上网时间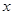 分钟之间的函数关系式,并在下图的坐标系中作出这两个函数的图象;
分钟之间的函数关系式,并在下图的坐标系中作出这两个函数的图象;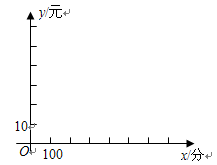
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com