
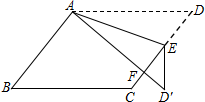
 如图,在平行四边形ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD'E处,AD'与CE交于点F.若∠B=48°,∠DAE=24°,则∠FED'的大小为36°.
如图,在平行四边形ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD'E处,AD'与CE交于点F.若∠B=48°,∠DAE=24°,则∠FED'的大小为36°. 分析 由平行四边形的性质得出∠D=∠B=48°,由折叠的性质得:∠D′=∠D=48°,∠EAD′=∠DAE=24°,由三角形的外角性质求出∠AEF=72°,与三角形内角和定理求出∠AED′=108°,即可得出∠FED′的大小.
解答 解:∵四边形ABCD是平行四边形,
∴∠D=∠B=48°,
由折叠的性质得:∠D′=∠D=48°,∠EAD′=∠DAE=24°,
∴∠AEF=∠D+∠DAE=48°+24°=72°,∠AED′=180°-∠EAD′-∠D′=108°,
∴∠FED′=108°-72°=36°;
故答案为:36°.
点评 本题考查了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理;熟练掌握平行四边形的性质和折叠的性质,求出∠AEF和∠AED′是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 仓库 产地 | C | D | 总计 |
| A | x吨 | 400吨 | |
| B | 300吨 | ||
| 总计 | 320吨 | 380 | 700吨 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com