
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:选择题
| A. | (1,-8) | B. | (1,-2) | C. | (-7,-1) | D. | (0,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
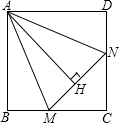 已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M、N,AH⊥MN于点H,如图MH=2,NH=3,求AH的长.
已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M、N,AH⊥MN于点H,如图MH=2,NH=3,求AH的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{{x^2}-4}}{x-2}$ | B. | $\frac{{4{x^2}+4x+1}}{2x+1}$ | C. | $\sqrt{4{x^3}}$ | D. | $\frac{{\sqrt{5}-1}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
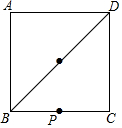 一个正方形的田地,BD所在线段种的是苹梨树,小明家在BC中点P处.他要从家出发摘苹果然后拿到位于点C处的集市上去卖,请在BD上找一点M,使得小明所走路径最短,即PM+CM最短,(要求:尺规作图,不写作法,保留作图痕迹)
一个正方形的田地,BD所在线段种的是苹梨树,小明家在BC中点P处.他要从家出发摘苹果然后拿到位于点C处的集市上去卖,请在BD上找一点M,使得小明所走路径最短,即PM+CM最短,(要求:尺规作图,不写作法,保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 分式$\frac{1}{x(x-1)}$有意义的条件是x≠0或x≠1 | |
| B. | 以长为3cm,5cm,7cm,10cm的四条线段中的三条线段为边,构成三角形的情况有1种 | |
| C. | -0.0000064用科学记数法表示为-6.4×10-6 | |
| D. | 等式(x2-9)0=1成立的条件是x=±3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com