
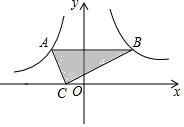
 如图,将含30°角的三角板ABC放置在坐标系中,此时直角顶点C的坐标是(-1,0),30°角的顶点B在反比例函数y=$\frac{2\sqrt{3}}{x}$位于第一象限内的图象上,顶点A在反比例函数y=$\frac{k}{x}$位于第二象限内的图象上,且AB∥x轴,则k的值是( )
如图,将含30°角的三角板ABC放置在坐标系中,此时直角顶点C的坐标是(-1,0),30°角的顶点B在反比例函数y=$\frac{2\sqrt{3}}{x}$位于第一象限内的图象上,顶点A在反比例函数y=$\frac{k}{x}$位于第二象限内的图象上,且AB∥x轴,则k的值是( )| A. | -2$\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | -1 | D. | -2 |
分析 作BD⊥x轴于点D,作AE⊥x轴于点E,由AB∥x轴知∠BCD=∠ABC=30°、∠ACE=∠BAC=60°,设点B坐标为(x,$\frac{2\sqrt{3}}{x}$),则BD=$\frac{2\sqrt{3}}{x}$、OD=x,由tan∠BCD=$\frac{BD}{CD}$求得x的值,即可知AE=BD=$\sqrt{3}$,再根据CE=$\frac{AE}{tan∠ACE}$=$\frac{\sqrt{3}}{\sqrt{3}}$=1得OE=2,从而得出k的值.
解答 解:如图,作BD⊥x轴于点D,作AE⊥x轴于点E,
∵AB∥x轴,
∴∠BCD=∠ABC=30°,∠ACE=∠BAC=60°,
设点B坐标为(x,$\frac{2\sqrt{3}}{x}$),
则BD=$\frac{2\sqrt{3}}{x}$,OD=x,
由tan∠BCD=$\frac{BD}{CD}$得$\frac{\sqrt{3}}{3}$=$\frac{\frac{2\sqrt{3}}{x}}{x+1}$,
解得:x=2或x=-3(舍),
∴AE=BD=$\sqrt{3}$,
在Rt△ACE中,∵CE=$\frac{AE}{tan∠ACE}$=$\frac{\sqrt{3}}{\sqrt{3}}$=1,
∴OE=2,
则k=-2$\sqrt{3}$,
故选:A
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.
如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,C,D是线段AB上的两点,AC=$\frac{5}{9}$BC,AD=$\frac{9}{5}$DB,若CD=2cm,求线段AB的长.
如图所示,C,D是线段AB上的两点,AC=$\frac{5}{9}$BC,AD=$\frac{9}{5}$DB,若CD=2cm,求线段AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 类别 | 频数 | 频率 |
| 助人为乐美德少年 | a | 0.20 |
| 自强自立美德少年 | 3 | b |
| 孝老爱亲美德少年 | 7 | 0.35 |
| 诚实守信美德少年 | 6 | c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com