
分析 (1)利用大量实验下的频率即为概率,进而求出即可;
(2)算出转一次转盘得到金额的平均数,与10比较即可.
解答 解:(1)P(不获奖)=$\frac{1000-50-100-200}{1000}$=$\frac{13}{20}$(或65%);
(2)∵转转盘的平均收益为:100×$\frac{50}{1000}$+50×$\frac{100}{1000}$+20×$\frac{200}{1000}$=14>10,
∴转转盘的方式更合算.
点评 此题主要考查了学生对简单几何概型的掌握情况,既避免了单纯依靠公式机械计算的做法,又体现了数学知识在现实生活、甚至娱乐中的运用,体现了数学学科的基础性.易错点是得到转一次转盘得到金额的平均数.


科目:初中数学 来源: 题型:填空题
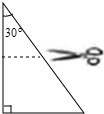 如图所示,是一张直角三角形纸片,其中有一个内角为30°,最小边长为2,点D、E分别是一条直角边和斜边的中点,先将纸片沿DE剪开,然后再将两部分拼成一个四边形,则所得四边形的周长是8或4+2$\sqrt{3}$.
如图所示,是一张直角三角形纸片,其中有一个内角为30°,最小边长为2,点D、E分别是一条直角边和斜边的中点,先将纸片沿DE剪开,然后再将两部分拼成一个四边形,则所得四边形的周长是8或4+2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 14 | B. | 140 | C. | 1400 | D. | 14000 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5y2-2y2=3 | B. | x6+x2=x8 | C. | (-a-b)2=a2-2ab+b2 | D. | $\sqrt{27}$-$\sqrt{12}$=$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com