
分析 (1)根据方程解的个数结合根的判别式,即可得出关于k的一元一次不等式,解不等式即可得出结论;
(2)当k=2时,原方程为x2-5x+5=0,设方程的两个为m、n,根据根与系数的关系找出m+n=5、mn=5,将$\sqrt{{m}^{2}+{n}^{2}}$变形为$\sqrt{(m+n)^{2}-2mn}$,再代入数据即可得出结论.
解答 解:(1)∵方程x2-(2k+1)x+k2+1=0有两个不相等的实数根,
∴△=[-(2k+1)]2-4×1×(k2+1)=4k-3>0,
∴k>$\frac{3}{4}$.
(2)当k=2时,原方程为x2-5x+5=0,
设方程的两个为m、n,
∴m+n=5,mn=5,
∴$\sqrt{{m}^{2}+{n}^{2}}$=$\sqrt{(m+n)^{2}-2mn}$=$\sqrt{15}$.
点评 本题考查了根的判别式以及根与系数的关系,熟练掌握当方程有两个不相等的实数根时△>0是解题的关键.


科目:初中数学 来源: 题型:解答题
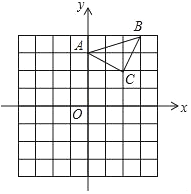 已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度).
已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com