
【题目】如图,在RtABC 中,ACB 90 , AC 3 ,BC 4 ,点 D在 AB上, AD AC , AF CD 交CD 于点 E ,交CB 于点 F ,则CF 的长是( )
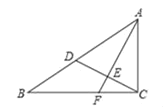
A. 2.5B. 2C. 1.8D. 1.5
【答案】D
【解析】
连接DF,由勾股定理求出AB=5,由等腰三角形的性质得出CE=DE,由线段垂直平分线的性质得出CF=DF,由SSS证明△ADF≌△ACF,得出∠ADF=∠ACF=∠BDF=90°,设CF=x,则DF=x,BF=4﹣x.在Rt△BDF中,由勾股定理得出方程,解方程即可.
连接DF,如图所示.
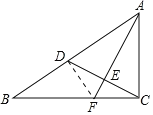
∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,∴AB![]() 5.
5.
∵AD=AC=3,AF⊥CD,∴CE=DE,BD=AB﹣AD=2,∴CF=DF.
在△ADF和△ACF中,∵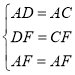 ,∴△ADF≌△ACF(SSS),∴∠ADF=∠ACF=90°,∴∠BDF=90°.设CF=x,则DF=x,BF=4﹣x.
,∴△ADF≌△ACF(SSS),∴∠ADF=∠ACF=90°,∴∠BDF=90°.设CF=x,则DF=x,BF=4﹣x.
在Rt△BDF中,由勾股定理得:DF2+BD2=BF2,即x2+22=(4﹣x)2,解得:x=1.5;∴CF=1.5.
故选D.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】 如图,△ABC是等边三角形,P是三角形内一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为18,则PD+PE+PF=( )
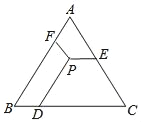
A. 18B. 9![]()
C. 6D. 条件不够,不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们新定义一种三角形:两边平方和等于第三边平方的两倍的三角形叫做奇异三角形.
(1)根据“奇异三角形”的定义,请你判断命题“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,点C是⊙O上一点(不与点A,B重合),D是半圆![]() 的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
求证:△ACE是奇异三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴与点
轴与点![]() 和
和![]() ,交
,交![]() 轴于点
轴于点![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,下列四个命题:
,下列四个命题:
①当![]() 时,
时,![]() ;
;
②若![]() ,则
,则![]() ;
;
③抛物线上有两点![]() 和
和![]() ,若
,若![]() ,且
,且![]() ,则
,则![]() ;
;
④点![]() 关于抛物线对称轴的对称点为
关于抛物线对称轴的对称点为![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,当
轴上,当![]() 时,四边形
时,四边形![]() 周长的最小值为
周长的最小值为![]() .
.
其中真命题的序号是( )
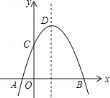
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一场篮球赛中,球员甲跳起投篮,已知球在![]() 处出手时离地面
处出手时离地面![]() ,与篮筐中心
,与篮筐中心![]() 的水平距离为
的水平距离为![]() ,当球运行的水平距离是
,当球运行的水平距离是![]() 时,达到最大高度
时,达到最大高度![]() (
(![]() 处),篮筐距地面
处),篮筐距地面![]() ,篮球运行的路线为抛物线(如图所示).
,篮球运行的路线为抛物线(如图所示).

![]() 建立适当的平面直角坐标系,并求出抛物线的解析式;
建立适当的平面直角坐标系,并求出抛物线的解析式;
![]() 判断此球能否投中?
判断此球能否投中?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个由传感器A控制的灯,要装在门上方离地面4.5m的墙上,任何东西只要移至该灯5m及5m内,灯就会自动发光,小明身高1.5m,他走到离墙_______的地方灯刚好发光.
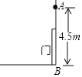
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色不同外,其它都一样),其中红球2个,蓝球1个,现在从中任意摸出一个红球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)第一次摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法求两次摸出的都是红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AE⊥BC于E,将△ABE沿AE所在直线翻折得△AEF,若AB=2,∠B=45°,则△AEF与菱形ABCD重叠部分(阴影部分)的面积为( ).
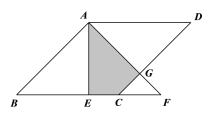
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 个边长为
个边长为![]() 的相邻正方形的一边均在同一直线上,点
的相邻正方形的一边均在同一直线上,点![]() ,
,![]() ,
,![]() ,…
,…![]() 分别为边
分别为边![]() ,
,![]() ,
,![]() ,…,
,…,![]() 的中点,
的中点,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,…
,…![]() 的面积为
的面积为![]() ,则
,则![]() ________.(用含
________.(用含![]() 的式子表示)
的式子表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com