
如图11,在直角梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,点
,点![]() 为坐标原点,点
为坐标原点,点![]() 在
在![]() 轴的正半轴上,对角线
轴的正半轴上,对角线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() .
.
(1)线段![]() 的长为 ,点
的长为 ,点![]() 的坐标为 ;
的坐标为 ;
(2)求△![]() 的面积;
的面积;
(3)求过![]() ,
,![]() ,
,![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(4)若点![]() 在(3)的抛物线的对称轴上,点
在(3)的抛物线的对称轴上,点![]() 为该抛物线上的点,且以
为该抛物线上的点,且以![]() ,
,![]() ,
,![]() ,
,![]() 四点为顶点的四边形为平行四边形,求点
四点为顶点的四边形为平行四边形,求点![]() 的坐标.
的坐标.
 |
解:(1)4![]() ;
;![]() .
.
(2)在直角梯形OABC中,OA=AB=4,![]()
∵ ![]() ∥
∥![]() ∴ △OAM∽△BCM
∴ △OAM∽△BCM
又 ∵ OA=2BC
∴ AM=2CM ,CM=![]() AC
AC
所以![]()
 (注:另有其它解法同样可得结果,正确得本小题满分.)
(注:另有其它解法同样可得结果,正确得本小题满分.)
(3)设抛物线的解析式为![]()
由抛物线的图象经过点![]() ,
,![]() ,
,![]() .所以
.所以

解这个方程组,得![]() ,
,![]() ,
,![]()
所以抛物线的解析式为 ![]()
(4)∵ 抛物线![]() 的对称轴是CD,
的对称轴是CD,![]()
① 当点E在![]() 轴的下方时,CE和OA互相平分则可知四边形OEAC为平行四边形,此时点F和点C重合,点F的坐标即为点
轴的下方时,CE和OA互相平分则可知四边形OEAC为平行四边形,此时点F和点C重合,点F的坐标即为点![]() ;
;
② 当点E在![]() 轴的下方,点F在对称轴
轴的下方,点F在对称轴![]() 的右侧,存在平行四边形
的右侧,存在平行四边形![]() ,
,![]() ∥
∥![]() ,且
,且![]() ,此时点F的横坐标为6,将
,此时点F的横坐标为6,将![]() 代入
代入![]() ,可得
,可得![]() .所以
.所以![]() .
.
同理,点F在对称轴![]() 的左侧,存在平行四边形
的左侧,存在平行四边形![]() ,
,![]() ∥
∥![]() ,且
,且![]() ,此时点F的横坐标为
,此时点F的横坐标为![]() ,将
,将![]() 代入
代入![]() ,可得
,可得![]() .所以
.所以![]() .
.
综上所述,点F的坐标为![]() ,
,![]()
![]() .
.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源:浙江省杭州市高桥初中教育集团2012届九年级下学期期初质量检测数学试题 题型:013
如图1,在直角梯形ABCD中,动点P从点B出发,沿BC→CD运动至点D停止.设点P运动的路程为x,△APB的面积为y,如果y关于x的函数图象如图2所示,则△BCD的面积是

A.16
B.15
C.11
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
如图11,在直角梯形ABCD中,已知AD∥BC,AB=3,AD=1,BC=6,∠A=∠B=90°. 设动点P、Q、R在梯形的边上,始终构成以P为直角顶点的等腰直角三角形,且△PQR的一边与梯形ABCD的两底平行.
(1) 当点P在AB边上时,在图中画出一个符合条件的△PQR (不必说明画法);
(2) 当点P在BC边或CD边上时,求BP的长.
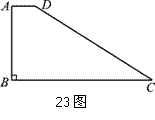 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图11,在直角梯形ABCD中,已知AD∥BC,AB=3,AD=1,BC=6,∠A=∠B=90°. 设动点P、Q、R在梯形的边上,始终构成以P为直角顶点的等腰直角三角形,且△PQR的一边与梯形ABCD的两底平行.
(1) 当点P在AB边上时,在图中画出一个符合条件的△PQR (不必说明画法);
(2) 当点P在BC边或CD边上时,求BP的长.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,在直角梯形ABCD中,动点P从点B出发,沿BC→CD运动至点D停止.设点P运动的路程为![]() ,△APB的面积为
,△APB的面积为![]() ,如果
,如果![]() 关于
关于![]() 的函数图象如图2所示,则△BCD的面积是( )
的函数图象如图2所示,则△BCD的面积是( )
A.16 B.15 C.11 D.5

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com