
| A. | x2+3x+5=0 | B. | $\sqrt{2x+1}$+3=0 | C. | $\frac{x}{x-2}$=$\frac{2}{x-2}$ | D. | -x2+x+3=0 |
分析 A和D:计算△的值,可以判断方程有无实数根;
B:二次根式≥0,根据二次根式的双重非负性进行判断即可;
C:分式方程要进行检验,判断有无实数根.
解答 解:A、x2+3x+5=0,
△=32-4×1×5=9-20<0,
∴方程无实数根;
B、$\sqrt{2x+1}$+3=0,
$\sqrt{2x+1}$=-3,
∴方程无实数根;
C、$\frac{x}{x-2}=\frac{2}{x-2}$,
则x=2,
当x=2时,分母x-2=0,
∴x=2不是原分式方程的解,
∴方程无实数根;
D、-x2+x+3=0,
△=12-4×(-1)×3=1+12>0,
∴方程有实数根;
故选D.
点评 本题考查了分式方程、无理方程和一元二次方程的根据的情况,明确利用根的判别式可以判定一元二次方程根的情况:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根;分式方程利用检验,将所求方程的解代入到最简公分母中,如果最简公分母为0,则不是原方程的解;无理方程利用:①$\sqrt{a}$≥0,②a≥0,进行判断.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:填空题
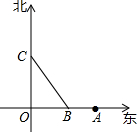 如图,甲船从点O出发,自南向北以40海里/时的速度行驶;乙船在点O正东方向120海里的A处,以30海里/时的速度自东向西行驶,经过2或$\frac{22}{25}$小时两船的距离为100海里.
如图,甲船从点O出发,自南向北以40海里/时的速度行驶;乙船在点O正东方向120海里的A处,以30海里/时的速度自东向西行驶,经过2或$\frac{22}{25}$小时两船的距离为100海里.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
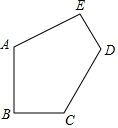 如图,已知AB=AE=$\sqrt{3}$,BC=DE=1,∠B=∠E=90°,∠A=120°,五边形ABCDE的面积是( )
如图,已知AB=AE=$\sqrt{3}$,BC=DE=1,∠B=∠E=90°,∠A=120°,五边形ABCDE的面积是( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 8 | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,数轴上点A,B,C分别表示有理数a,b,c,若ac<0,a+b>0,则原点位于( )
如图,数轴上点A,B,C分别表示有理数a,b,c,若ac<0,a+b>0,则原点位于( )| A. | 点A的左侧 | B. | 点A与点B之间 | C. | 点B与点C之间 | D. | 在点C的右侧 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
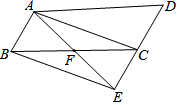 如图,延长平行四边形ABCD的边DC到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.
如图,延长平行四边形ABCD的边DC到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3×10-9m | B. | 3×10-10m | C. | 3×10-11m | D. | 0.3×10-9m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com