Question

某企业引进一条农产品加工生产线，该生产线投产后，从第1年到第x年的维修费用累计为w（万元），且w=ax²+bx，若第1、2年的维修费用累计为6万元，第1、2、3年的维修费用累计为12万元．
（1）试求w的解析式；
（2）已知该企业引进这条生产线时投资100万元，预计投产后平均每年的产值为33万元，设这个企业从第一年到第x年累计获得的利润总和为y万元，
①若只考虑投资与维修费用这两顶支出，试求y关于x的函数关系式，并求这条生产线投产后的第几年能使企业获得的累计利润总和最多？最多的累计利润总和是多少万元？
②利用①中的函数及其图象分折，该企业投产后，大约在哪几年内能盈利？

Answer 1

分析：（1）分别将x=2，w=6和x=3，w=12分别代入w=ax²+bx中计算可得a、b的值，那么解析式可求；
（2）①根据盈利、投入和维修费用三项列出y关于x的函数关系式，将二次函数关系式进行适当变形，找出抛物线顶点，即可知道这条生产线投产后的第几年能使企业获得的累计利润总和最多，并可求出最多的累计利润总和；
②根据上面步骤可画出二次函数的抛物线图象，根据抛物线的开口、顶点和与x轴的交点来判断该企业投产后，大约在哪几年内能盈利．

解答：解：（1）将x=2，w=6和x=3，w=12分别代入w=ax²+bx中计算得，
a=1，b=1，
所以w的解析式为：w=x²+x；

（2）①由题意得y关于x的函数关系式为：
y=33x-100-x²-x，
则y=-（x-16）²+156（x＞0），
∴投产后的第16年能使企业盈得的累计利润总和最多，最多的累计利润总和是：156万元．
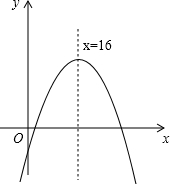
②函数y=-（x-16）²+156的草图如图，函数图象的对称轴是x=16，顶点为（16，156），开口向下，在对称轴左边y（累计获得的利润总和）随着x的增大而增大，在对称轴右边y（累计获得的利润总和）则随着x的增大而减少．
令y=33x-100-x²-x=0，
解得x1=16-2

39

≈3.51，x2=16+2

39

（舍去）．
根据上述分析可得这个企业投产后大约在第4年到第16年内盈利．

点评：本题考查的是二次函数在实际生活中的应用，解此类题的关键是根据题意确定出二次函数的解析式，然后确定其最大值，实际问题中自变量x的取值要使实际问题有意义，因此在求二次函数的最值时，一定要注意自变量x的取值范围．