
【题目】阅读理解:
方法准备:
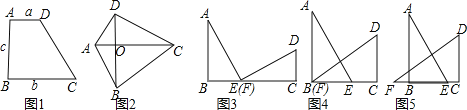
我们都知道:如图1,在四边形ABCD中,AD∥BC,∠B=90°,若AD=a,BC=b,AB=c,那么四边形ABCD的面积S=![]() .
.
如图2,在四边形ABCD中,两条对角线AC⊥BD,垂足为O,则四边形ABCD的面积=![]() AC×OD+
AC×OD+![]() AC×OB=
AC×OB=![]() AC×(OD+OB)=
AC×(OD+OB)=![]() AC×BD.
AC×BD.
解决问题:
(1)我们以a、b 为直角边,c为斜边作两个全等的直角△ABE与△FCD,再拼成如图3所示的图形,使B,E,F,C四点在一条直线上(此时E,F重合),可知△ABE≌△FCD,AE⊥DF. 请你证明:a2+b2=c2.
(2)固定△FCD,再将△ABE沿着BC平移到如图4所示的位置(此时B,F重合),请你继续证明:a2+b2=c2.
(3)当△ABE平移到如图5的位置,结论a2+b2=c2还成立吗?如果成立,请写出证明过程;如果不成立,请说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)成立,理由见解析.
【解析】
试题分析:(1)连接AD,由四边形ABCD的面积=△ABE的面积+△FCD的面积+△ADE的面积,得出![]() (a+b)2=
(a+b)2=![]() ab×2+
ab×2+![]() c2,即可得出结论;
c2,即可得出结论;
(2)连接AD、DE,四边形ABCD的面积=四边形ABED的面积+△DCE的面积,得出![]() (a+b)×a=
(a+b)×a=![]() c2+
c2+![]() b(a﹣b),即可得出结论;
b(a﹣b),即可得出结论;
(3)连接AF、AD、DE,设CE=x,则BE=b,FB=a﹣b﹣x,由△ABF的面积+四边形ABCD的面积=四边形AFED的面积+△CDE的面积,得出![]() a(a﹣b﹣x)+
a(a﹣b﹣x)+![]() (a+b)(b+x)=
(a+b)(b+x)=![]() c2+
c2+![]() bx,即可得出结论.
bx,即可得出结论.
(1)证明:连接AD,如图1所示:
则四边形ABCD是直角梯形,
∴四边形ABCD的面积=![]() (a+b)(a+b)=
(a+b)(a+b)=![]() (a+b)2,
(a+b)2,
∵四边形ABCD的面积=△ABE的面积+△FCD的面积+△ADE的面积,
即![]() (a+b)2=
(a+b)2=![]() ab×2+
ab×2+![]() c2,
c2,
化简得:(a+b)2=2ab+c2,
∴a2+b2=c2;
(2)证明:连接AD、DE,如图2所示:
则四边形ABCD的面积=四边形ABED的面积+△DCE的面积,
即![]() (a+b)×a=
(a+b)×a=![]() c2+
c2+![]() b(a﹣b),
b(a﹣b),
化简得:ab+a2=c2+ab﹣b2,
∴a2+b2=c2;
(3)成立;理由如下:
连接AF、AD、DE,如图3所示:
设CE=x,则BE=b,FB=a﹣b﹣x,
∵△ABF的面积+四边形ABCD的面积=四边形AFED的面积+△CDE的面积,
∴![]() a(a﹣b﹣x)+
a(a﹣b﹣x)+![]() (a+b)(b+x)=
(a+b)(b+x)=![]() c2+
c2+![]() bx,
bx,
化简得:a2﹣ab﹣ax+ab+ax+b2+bx=c2+bx,
∴a2+b2=c2.





 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,求抛物线经过A(1,0),C(0,3)两点,与x轴交于A、B两点.
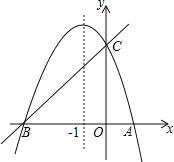
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在该抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为该抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.(提示:若平面直角坐标系内两点P(x1,y1)、Q(x2,y2),则线段PQ的长度PQ=![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
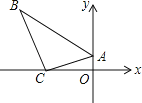
【题目】一块直角三角板ABC按如图放置,顶点A的坐标为(0,1),直角顶点C的坐标为(﹣3,0),∠B=30°,则点B的坐标为( )
A.(﹣3﹣![]() ,3)
,3)
B.(﹣3﹣![]() ,3
,3![]() )
)
C.(﹣![]() ,3)
,3)
D.(﹣![]() ,3
,3![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解一路段车辆行驶速度的情况,交警统计了该路段上午7::0至9:00来往车辆的车速(单位:千米/时),并绘制成如图所示的条形统计图.这些车速的众数、中位数分别是( )
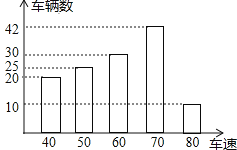
A.众数是80千米/时,中位数是60千米/时
B.众数是70千米/时,中位数是70千米/时
C.众数是60千米/时,中位数是60千米/时
D.众数是70千米/时,中位数是60千米/时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C在同一直线上,△ABD和△BCE都是等边三角形.则在下列结论中:①AP=DQ,②EP=EC,③PQ=PB,④∠AOB=∠BOC=∠COE.正确的结论是 (填写序号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com